Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maxwell, George
1971.
On double commutators.
Linear Algebra and its Applications,
Vol. 4,
Issue. 3,
p.
283.
Long, J.P.
and
Cullen, C.G.
1974.
Intrinsic functions on real semisimple algebras.
Linear Algebra and its Applications,
Vol. 9,
Issue. ,
p.
199.
Armendariz, Efraim P.
and
Park, Jae Keol
1983.
The double centralizer theorem for division algebras.
Israel Journal of Mathematics,
Vol. 45,
Issue. 1,
p.
63.
Farenick, Douglas R.
and
Pidkowich, Barbara A.F.
2003.
The spectral theorem in quaternions.
Linear Algebra and its Applications,
Vol. 371,
Issue. ,
p.
75.
Chuang, Chen-Lian
and
Lee, Tsiu-Kwen
2014.
The Double Centralizer Theorem for Semiprime Algebras.
Algebras and Representation Theory,
Vol. 17,
Issue. 4,
p.
1277.

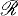 we shall denote by
we shall denote by 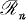 the ring of all
the ring of all 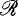 and by
and by 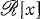 the set of all polynomials in
the set of all polynomials in 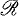 .
. will denote the non-commutative four-dimensional division algebra of real quaternions with 1,
will denote the non-commutative four-dimensional division algebra of real quaternions with 1,