Article contents
Compact Perturbations of Reflexive Algebras
Published online by Cambridge University Press: 20 November 2018
Extract
In this paper we study lattice properties of operator algebras which are invariant under compact perturbations. It is easy to see that if 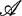 and
and 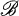 are two operator algebras with
are two operator algebras with 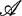 contained in
contained in 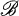 , then the reverse inclusion holds for their lattices of invariant subspaces. We will show that in certain cases, the assumption thats
, then the reverse inclusion holds for their lattices of invariant subspaces. We will show that in certain cases, the assumption thats 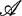 is contained in
is contained in 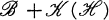 , where
, where 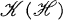 is the ideal of compact operators, implies that the lattice of
is the ideal of compact operators, implies that the lattice of 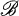 is “approximately” contained in the lattice of
is “approximately” contained in the lattice of 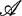 . In particular, supposed
. In particular, supposed 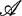 and
and 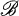 are reflexive and have commutative subspace lattices containing “enough” finite dimensional elements. We show (Corollary 2.8) that if
are reflexive and have commutative subspace lattices containing “enough” finite dimensional elements. We show (Corollary 2.8) that if 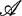 is unitarily equivalent to a subalgebra of
is unitarily equivalent to a subalgebra of 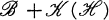 , then there is a unitary operator which carries all “sufficiently large” subspaces in lat
, then there is a unitary operator which carries all “sufficiently large” subspaces in lat 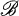 into lat
into lat 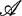 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 1
- Cited by


