No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
For an integer n > 1, the letters U and Bn denote the open unit disc in C and the open euclidean unit ball in Cn, respectively. It is known that the homogeneous polynomials
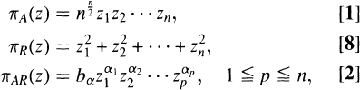
where bα is chosen so that 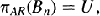 , have the following pull-back property:
, have the following pull-back property:
If g ∈ ℬ(U) the Block space, then 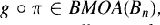 , the space of hoiomorphic functions on Bn of bounded mean oscillation, for
, the space of hoiomorphic functions on Bn of bounded mean oscillation, for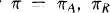 and
and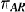 .
.