Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T22:28:25.177Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence Relations for Shimura Varieties Associated with GU(n–1, 1)

Published online by Cambridge University Press:  20 November 2018

Jean-Stefan Koskivirta
Jean-Stefan Koskivirta*
Affiliation:
Strasbourg University. e-mail: jeanstefan.koskivirta@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove the congruence relation for the 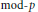$\bmod -p$ reduction of Shimura varieties associated with a unitary similitude group 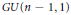$GU(n\,-\,1,\,1)$ over 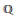$\mathbb{Q}$ when 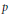$p$ is inert and 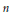$n$ odd. The case when 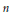$n$ is even was obtained by T. Wedhorn and O. Bültel, as a special case of a result of B. Moonen, when the 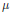$\mu$–ordinary locus of the 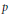$p$–isogeny space is dense. This condition fails in our case. We show that every supersingular irreducible component of the special fiber of 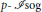$p-I\text{sog}$ is annihilated by a degree one polynomial in the Frobenius element 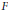$F$, which implies the congruence relation.

Keywords

11G1814G3514K10Shimura varietiescongruence relation
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 6 , 01 December 2014 , pp. 1305 - 1326
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Blasius, D. and Rogawski, J. D., Zeta functions of Shimura varieties. In: Motives (Seattle,WA, 1991),Proc. Sympos. Pure Math., 55, American Mathematical Society, 1994, pp. 525–571.Google Scholar
[2] Bültel, O., The congruence relation in the non-PEL case. J. Reine Angew. Math. 544 (2002), 133–159.Google Scholar
[3] Bültel, O. and Wedhorn, T., Congruence relations for Shimura varieties associated to some unitary groups. J. Inst. Math. Jussieu 5(2006), no. 2, 229–261.http://dx.doi.org/10.1017/S1474748005000253 Google Scholar
[4] Brian, C., Gross–Zagier revisited. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ., 49, Cambridge University Press, Cambridge, 2004, pp. 67–163.Google Scholar
[5] Faltings, G. and Chai, C.-L., Degeneration of abelian varieties Ergebnisse der Math., 22, Springer-Verlag, Berlin, 1990.Google Scholar
[6] Fulton, W., Intersection theory. Ergebnisse Der Mathematik Und Ihrer Grenzgebiete, 3. Folge, Bd. 2, Springer-Verlag GmbH, 1998.Google Scholar
[7] Grothendieck, A., Éléments de géométrie algébrique. IV. étude locale des schmas et des morphismes de schémas. III. Inst. Hautes Études Sci. Publ. Math. 28(1966), 1–255.Google Scholar
[8] Grothendieck, A., Groupes de Barsotti-Tate et cristaux de Dieudonné. Séminaire de Mathématiques Supérieures, 45, Les Presses de l’Université de Montréal, Montreal, Que., 1974.Google Scholar
[9] Kottwitz, R. E., Points on some Shimura varieties over finite fields. J. Amer. Math. Soc. 5(1992), no. 2, 373–444. http://dx.doi.org/10.1090/S0894-0347-1992-1124982-1 Google Scholar
[10] Milne, J. S., Introduction to Shimura varieties. In: Harmonic analysis, the trace formula, and Shimura varieties, Clay Math. Proc., 4, American Mathematical Society, 2005, pp. 265–378.Google Scholar
[11] Moonen, B., Serre–Tate theory for moduli spaces of PEL type. Ann. Sci. École Norm. Sup. (4) 37(2004), 223–269.Google Scholar
[12] Rapoport, M. and Zink, Th., Period spaces for p-divisible groups. Annals of Mathematics Studies, 141, Princeton University Press, Princeton, 1996.Google Scholar
[13] Vollaard, I., The supersingular locus of the Shimura variety forGU(1,s). Canad. J. Math. 62(2010), no. 3, 668–720.http://dx.doi.org/10.4153/CJM-2010-031-2 Google Scholar
[14] Vollaard, I. and Wedhorn, T, The supersingular locus of the Shimura variety of GU(1,n – 1) II. Invent. Math. 184(2011), no. 3, 591–627 http://dx.doi.org/10.1007/s00222-010-0299-y.Google Scholar
[15] Wedhorn, T., Ordinariness in good reductions of Shimura varieties of PEL-type. Ann. Sci. École Norm. Sup. (4) 32(1999), no. 5, 575–618.Google Scholar
[16] Wedhorn, T., Congruence relations on some Shimura varieties. J. Reine Angew. Math. 524(2000), 43–71.Google Scholar