Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-27T18:31:54.885Z Has data issue: false hasContentIssue false
  • English
  • Français

Conilpotency and Weak Category

Published online by Cambridge University Press:  20 November 2018

C. S. Hoo
C. S. Hoo*
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ƒ : X → Y be a map and let e′: Y → ΩΣY be the usual embedding. Then we prove the following results.

Theorem 1. cat ƒ = cat(e′ƒ), w cat ƒ = w cat(e′ƒ) if Y is an H-space.

Theorem 2. conil ƒ = w Σ cat(e′ƒ) ≦ Σ w cat(e′ƒ) ≦ w cat(e′ƒ), where Σ the suspension functor. If we take X = Y and ƒ= lx, this result yields conil X ≦ w cat e', a result due to Ganea, Hilton, and Peterson(4).

Theorem 3. Suppose that Y is (m– 1)-connected and

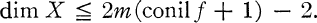
Then conil ƒ = w Σ cat (e′ƒ) = Σ w cat(e′ƒ) = w cat(e′ƒ).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 730 - 734
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Berstein, I. and Ganea, T., Homotopical nilpotency, Illinois J. Math. 5 (1961), 99–130.Google Scholar
2. Berstein, I. and Hilton, P. J., Homomorphisms of homotopy structures, Topologie et géométrie différentielle, Séminaire Ehresmann, April, 1963 (Inst. Henri Poincaré, Paris, 1963).Google Scholar
3. Ganea, T., On some numerical homotopy invariants, Proc. Internat. Congress Math., 1962, pp. 467–472 (Inst. Mittag-Leffler, Djursholm, Sweden, 1963).Google Scholar
4. Ganea, T., Hilton, P. J., and Peterson, F. P., On the homotopy-commutativity of loop-spaces and suspensions, Topology 1 (1962), 133–141.Google Scholar
5. Peterson, F. P., Numerical invariants of homotopy type, Colloquium on algebraic topology, pp. 79–83, Aarhus Universitet, 1962.Google Scholar
5. Stasheff, J., On homotopy abelian H-spaces, Proc. Cambridge Philos. Soc. 57 (1961), 734–745.Google Scholar