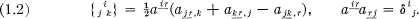Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jeffries, Clark
1972.
0-deformable $(1,\,1)$-tensor fields.
Journal of Differential Geometry,
Vol. 7,
Issue. 3-4,
1972.
Lie Gronps, Principal Bundles, and Characteristic Classes.
Vol. 47,
Issue. ,
p.
511.
Mazur, P. O.
and
Sokolowski, L. M.
1986.
Teleparallelism as a universal connection on null hypersurfaces in general relativity.
General Relativity and Gravitation,
Vol. 18,
Issue. 8,
p.
781.


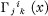 such that the covariant derivative, defined by
such that the covariant derivative, defined by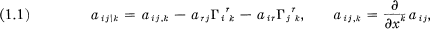
 is symmetric and positive definite. A solution connection of the problem is then given by the Christoffel symbols
is symmetric and positive definite. A solution connection of the problem is then given by the Christoffel symbols