Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T05:54:10.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Consistency of Moment Systems

Published online by Cambridge University Press:  20 November 2018

A. S. Lewis
A. S. Lewis*
Affiliation:
Department of Combinatorics and Optimization, University of Waterloo, Waterloo, Ontario, N2L 3G1 e-mail: aslewis@orion.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

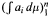An important question in the study of moment problems is to determine when a fixed point in ℝn lies in the moment cone of vectors , with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.

Keywords

49A5590C2565K0549B27moment problemconvex analysisdualitymaximum entropypartially finite programconstraint qualification
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 5 , 01 October 1995 , pp. 995 - 1006
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Borwein, J.M. and Lewis, A.S., Duality relationships for entropy-like minimization problems, SI AM J. Control Optim. 29(1991), 325–338.Google Scholar
2. Borwein, J.M., Partially finite convex programming, Part I, Duality theory, Math. Programming B 57(1992), 15–48.Google Scholar
3. Borwein, J.M., Partially-finite programming in L1 and the existence of maximum entropy estimates, SIAM J. Optim. 2(1993), 248–267.Google Scholar
4. Dacunha-Castelle, D. and Gamboa, F., Maximum d'entropie et problème des moments, Ann. Inst. H. Poincaré 26(1990), 567–596.Google Scholar
5. Gamboa, F., Méthode du Maximum d'Entropie sur la Moyenne et Applications, PhD thesis, Université Paris Sud, Centre d'Orsay, 1989.Google Scholar
6. Gamboa, F. and Gassiat, E., Maximum d'entropie et problème des moments cas multidimensionnel, Statistics Laboratory, University of Orsay, France, 1990. preprint.Google Scholar
7. Gamboa, F., Extension of the maximum entropy method on the mean and a Bayesian interpretation of the method, Statistics Laboratory, University of Orsay, France, 1991. preprint.Google Scholar
8. Gamboa, F., M.E.M. techniques for solving moment problems, Statistics Laboratory, University of Orsay, France, 1991. preprint.Google Scholar
9. Glashoff, K. and Gustafson, S.-A., Linear optimization and approximation, Springer-Verlag, New York, 1983.Google Scholar
10. Karlin, S. and Studden, W.J., Tchebycheff systems: with applications in analysis and statistics, Wiley- Interscience, New York, 1966.Google Scholar
11. Krein, M.G. and Nudel'man, A.A., The Markov moment problem and extremal problems, Amer. Math. Soc, 1977.Google Scholar
12. Lewis, A.S., Consistency of moment systems, Technical Report CORR 93-23, University of Waterloo, 1993.Google Scholar
13. Rockafellar, R.T., Duality and stability in extremum problems involving convex functions, Pacific J. Math. 21(1967), 167–187.Google Scholar
14. Rockafellar, R.T., Convex Analysis, Princeton University Press, Princeton, New Jersey, 1970.Google Scholar
15. Rockafellar, R.T., Conjugate duality and optimization, SI AM, Philadelphia, Pennsylvania, 1974.Google Scholar
16. Schaefer, H.H., Banach lattices and positive operators, Springer-Verlag, Berlin, 1974.Google Scholar