Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T07:06:10.029Z Has data issue: false hasContentIssue false
  • English
  • Français

Constrained Approximation with Jacobi Weights

Published online by Cambridge University Press:  20 November 2018

Kirill Kopotun ,
Dany Leviatan  and
Igor Shevchuk
Kirill Kopotun
Affiliation:
Department of Mathematics, University of Manitoba, Winnipeg, Manitoba e-mail: kopotunk@cc.umanitoba.ca
Dany Leviatan
Affiliation:
Raymond and Beverly Sackler School of Mathematical Sciences, Tel Aviv University, Tel Aviv, Israel e-mail: leviatan@post.tau.ac.il
Igor Shevchuk
Affiliation:
Faculty of Mechanics and Mathematics, National Taras Shevchenko University of Kyiv, Kyiv, Ukraine e-mail: shevchuk@univ.kiev.ua
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we prove that for 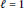$\ell \,=\,1$ or 2 the rate of best 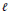$\ell $ - monotone polynomial approximation in the 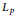${{L}_{p}}$ norm 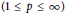$\left( 1\,\le \,p\,\le \,\infty \right)$ weighted by the Jacobi weight 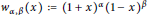${{w}_{\alpha ,\,\beta }}\left( x \right)\,:=\,{{\left( 1\,+\,x \right)}^{\alpha }}{{\left( 1\,-\,x \right)}^{\beta }}$ with 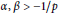$\alpha ,\,\beta \,>\,-1/p$ if 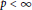$p\,<\,\infty $ , or 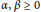$\alpha ,\,\beta \,\ge \,0$ if 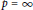$p\,=\,\infty $ , is bounded by an appropriate 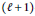$\left( \ell \,+\,1 \right)$ -st modulus of smoothness with the same weight, and that this rate cannot be bounded by the $\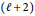left( \ell \,+\,2 \right)$ -nd modulus. Related results on constrained weighted spline approximation and applications of our estimates are also given.

Keywords

41A2941A1041A1541A1741A25constrained approximationJacobi weightsweighted moduli of smoothnessexact estimatesexact orders
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 1 , 01 February 2016 , pp. 109 - 128
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] De Bonis, M. C., Mastroianni, G., and Russo, M. G., Polynomial approximation with special doubling weights. Acta Sci. Math. (Szeged) 69(2003), no. 1-2, 159–184.Google Scholar
[2] De Bonis, M. C., Mastroianni, G., and Viggiano, M., K-functionals, moduli of smoothness and weighted best approximation of the semiaxis. In: Functions, series, operators (Budapest, 1999), Jénos Bolyai Math. Soc. Budapest, 2002, pp. 181–211.Google Scholar
[3] DeVore, R. A., Hu, Y. K., and Leviatan, D., Convex polynomial and spline approximation in Lp, 0 < p < ∞. Constr. Approx. 12(1996), 409–422.http://dx.doi.org/10.1007/BF02433051 Google Scholar
[4] Ditzian, Z., Polynomial approximation and wr ϕ twenty years later. Surv. Approx. Theory 3(2007), 106–151.Google Scholar
[5] Ditzian, Z. and Totik, V., Moduli of smoothness. Springer Series in Computational Mathematics, 9, Springer-Verlag, New York, 1987.Google Scholar
[6] Kopotun, K. A., Pointwise and uniform estimates for convex approximation of functions by algebraic polynomials. Constr. Approx. 10(1994), no. 2,153–178.http://dx.doi.Org/10.1007/BF01263061 Google Scholar
[7] Kopotun, K. A., Weighted moduli of smoothness of k-monotone functions and applications. J. Approx. Theory 192(2015), 102–131. http://dx.doi.Org/10.1016/j.jat.2O14.11.006 Google Scholar
[8] Kopotun, K. A., Polynomial approximation with doubling weights. Acta Math. Hungar. 146(2015), no. 2, 496–535.http://dx.doi.Org/10.1007/s10474-015-0519-4 Google Scholar
[9] Kopotun, K. A., Polynomial approximation with doubling weights having finitely many zeros and singularities. J. Approx. Theory 198(2015), 24–62.http://dx.doi.Org/10.1016/j.jat.2O15.05.003 Google Scholar
[10] Kopotun, K. A., Leviatan, D., Prymak, A., and Shevchuk, I. A., Uniform and pointwise shape preserving approximation by algebraic polynomials. Surv. Approx. Theory 6(2011), 24–74.Google Scholar
[11] Ky, N. X., On approximation of functions by polynomials with weight. Acta Math. Hungar. 59(1992), no. 1–2, 49–58.http://dx.doi.org/10.1007/BF00052090 Google Scholar
[12] Mastroianni, G. and Totik, V., Best approximation and moduli of smoothness for doubling weights. J. Approx. Theory 110(2001), no. 2,180–199.http://dx.doi.Org/10.1006/jath.2000.3546 Google Scholar
[13] Shvedov, A. S., Orders of coapproximations of functions by algebraic polynomials. (Russian) Mat. Zametki 29(1981), no. 1,117–130,156.Google Scholar