Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T06:10:58.595Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence Factors and Compactness in Weighted Convolution Algebras

Published online by Cambridge University Press:  20 November 2018

Fereidoun Ghahramani  and
Sandy Grabiner
Fereidoun Ghahramani
Affiliation:
Dept. of Mathematics University of Manitoba Winnipeg, Manitoba R3T 2N2
Sandy Grabiner
Affiliation:
Dept. of Mathematics Pomona College Claremont, CA 91711-6348 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study convergence in weighted convolution algebras 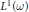${{L}^{1}}\left( \omega \right)$ on 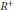${{R}^{+}}$, with the weights chosen such that the corresponding weighted space 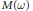$M\left( \omega \right)$ of measures is also a Banach algebra and is the dual space of a natural related space of continuous functions. We determine convergence factor 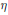$\eta $ for which weak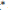$*$-convergence of 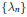$\left\{ {{\text{ }\!\!\lambda\!\!\text{ }}_{n}} \right\}$ to 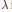$\text{ }\!\!\lambda\!\!\text{ }$ in 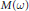$M\left( \omega \right)$ implies norm convergence of 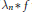${{\text{ }\!\!\lambda\!\!\text{ }}_{n}}*f$ to 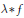$\text{ }\!\!\lambda\!\!\text{ *}f$ in 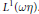${{L}^{1}}\left( \omega \eta \right)$. We find necessary and sufficent conditions which depend on 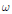$\omega$ and 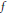$f$ and also find necessary and sufficent conditions for 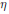$\eta$ to be a convergence factor for all 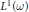${{L}^{1}}\left( \omega \right)$ and all 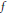$f$ in 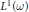${{L}^{1}}\left( \omega \right)$. We also give some applications to the structure of weighted convolution algebras. As a preliminary result we observe that 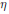$\eta$ is a convergence factor for 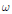$\omega$ and 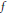$f$ if and only if convolution by 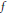$f$ is a compact operator from 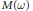$M\left( \omega \right)$ (or 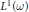${{L}^{1}}\left( \omega \right)$) to 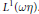${{L}^{1}}\left( \omega \eta \right)$.

Keywords

43A1043A1546J4546J99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 303 - 323
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bade, W. G. and Dales, H. G., Norms and ideals in radical convolution algebras. J. Funct. Anal. 41 (1981), 77–109.Google Scholar
[2] Bade, W. G. and Dales, H. G., Continuity of derivations from radical convolution algebras. Studia Math. 95 (1989), 60–91.Google Scholar
[3] Dales, H. G. and McClure, J. P., Nonstandard ideals in radical convolution algebras on a half-line. Canad. J. Math. 39 (1987), 309–321.Google Scholar
[4] Day, M. M., Normed Linear Spaces. 3rd edition, Ergeb. der Math. 21, Springer-Verlag, New York, 1973.Google Scholar
[5] Detre, P., Multipliers of Weighted Lebesgue Spaces. Ph.D. dissertation, Univ. of Calif., Berkeley, 1988.Google Scholar
[6] Dunford, N. and Schwartz, J. T., Linear Operators, Part I. Wiley Interscience, New York, 1958.Google Scholar
[7] Ghaharamani, F. and Grabiner, S., Standard homomorphisms and convergent sequences in weighted convolution algebras. Illinois J. Math. 36 (1992), 505–527.Google Scholar
[8] Ghaharamani, F. and Grabiner, S., The Lp theory of standard homomorphisms. Pacific J. Math. 168 (1995), 49–60.Google Scholar
[9] Ghahramani, F., Grabiner, S. and McClure, J. P., Standard homomorphisms and regulated weights on weighted convolution algebras. J. Funct. Anal. 91 (1990), 278–286.Google Scholar
[10] Grabiner, S., Weighted convolution algebras on the half line. J. Math. Anal. Appl. 83 (1981), 521–553.Google Scholar
[11] Grabiner, S., Homomorphisms and semigroups in weighted convolution algebras. Indiana Univ. Math. J. 37 (1988), 589–615.Google Scholar
[12] Grabiner, S., Weighted convolution algebras and their homomorphisms. In: Functional Analysis and Operator Theory, Banach Center Publications 30(1994), Polish Acad. of Sci.,Warsaw, 175–190.Google Scholar
[13] Hille, E. and Phillips, R. S., Functional Analysis and Semi-groups. Amer. Math. Soc. Colloq. Public 31, Providence, RI, 1957.Google Scholar