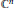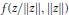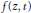Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hamada, Hidetaka
Kohr, Gabriela
Mocanu, Petru T.
and
Şerb, Ioan
2010.
Convex subordination chains and injective mappings in Cn.
Journal of Mathematical Analysis and Applications,
Vol. 364,
Issue. 1,
p.
32.
Duren, Peter
Graham, Ian
Hamada, Hidetaka
and
Kohr, Gabriela
2010.
Solutions for the generalized Loewner differential equation in several complex variables.
Mathematische Annalen,
Vol. 347,
Issue. 2,
p.
411.