Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T15:13:55.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution Powers of Salem MeasuresWith Applications

Published online by Cambridge University Press:  20 November 2018

Xianghong Chen  and
Andreas Seeger
Xianghong Chen
Affiliation:
Department of Mathematical Sciences, University of Wisconsin-Milwaukee, Milwaukee, WI 53211, USA e-mail: chen242@umw.edu
Andreas Seeger
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, Madison, WI 53706, USA e-mail: seeger@math.wisc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

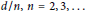We study the regularity of convolution powers for measures supported on Salem sets, and prove related results on Fourier restriction and Fourier multipliers. In particular we show that for $\alpha $ of the form $d\,/\,n,\,n\,=\,2,3,...$ there exist $\alpha $-Salem measures for which the 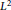${{L}^{2}}$ Fourier restriction theorem holds in the range 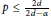$p\,\le \,\frac{2d}{2d\,-\,\alpha }$. The results rely on ideas of Körner. We extend some of his constructions to obtain upper regular $\alpha $-Salem measures, with sharp regularity results for $n$-fold convolutions for all 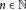$n\,\in \,\mathbb{N}$.

Keywords

42A8542B9942B1542A61convolution powersFourier restrictionSalem setsSalem measuresrandom sparse setsFourier multipliers of Bochner-Riesz type.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 2 , 01 April 2017 , pp. 284 - 320
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bak, J.-G and Seeger, A., Extensions of the Stein-Tomas theorem. Math. Res. Lett. 18(2011), no. 4,767–781. http://dx.doi.Org/10.4310/MRL.2011.v18.n4.a14 Google Scholar
[2] Bluhm, C., Random recursive construction of Salem sets. Ark. Mat. 34(1996), no. 1, 51–63. http://dx.doi.org/10.1007/BF02559506 Google Scholar
[3] Bluhm, C., On a theorem of Kaufman: Cantor-type construction of linear fractal Salem sets. Ark. Mat. 36(1998), no. 2, 307–316. http://dx.doi.org/10.1007/BF02384771 Google Scholar
[4] Bourgain, J., Bounded orthogonal systems and the A(p)-set problem. Acta Math. 162(1989), no. 3-4, 227–245. http://dx.doi.org/10.1007/BF02392838 Google Scholar
[5] Chan, V., On convolution squares of singular measures. Master's Thesis, University of Waterloo, 2010.Google Scholar
[6] Chen, X., A Fourier restriction theorem based on convolution powers. Proc. Amer. Math. Soc. 142(2014), no. 11, 3897–3901. http://dx.doi.org/10.1090/S0002-9939-2014-12148-4 Google Scholar
[7] Chen, X.,Restriction of the Fourier transform to Salem sets. Ph.D. Thesis, University of Wisconsin-Madison 2015.Google Scholar
[8] Chen, X., Sets of Salem type and sharpness of the L2-Fourier restriction theorem. Trans. Amer.Math. Soc. 368(2016), no.3, 1959–1977. http://dx.doi.Org/10.1090/tran/6396 Google Scholar
[9] Erdös, P. and Rényi, A., A probabilistic approach to problems of diophantine approximation. Illinois J. Math. 1(1957), 303–315.Google Scholar
[10] Fefferman, C., Inequalities for strongly singular convolution operators. Acta Math. 124(1970), 9–36. http://dx.doi.org/10.1007/BF02394567 Google Scholar
[11] Hambrook, K., Explicit Salem sets and applications to metrical Diophantine approximation. arxiv:1604.00411.Google Scholar
[12] Hambrook, K. and Laba, I., On the sharpness of Mockenhaupt's restriction theorem. Geom. Funct.Anal. 23(2013), no. 4, 1262–1277. http://dx.doi.org/10.1007/s00039-013-0240-9 Google Scholar
[13] Hambrook, K.,Sharpness of the Mockenhaupt-Mitsis-Bak-Seeger restriction theorem in higher dimensions.arxiv:5O9.O5912.Google Scholar
[14] Hoeffding, W., Probability inequalities for sums of bounded random variables. J. Amer. Statist.Assoc. 58(1963), 13–30. http://dx.doi.org/10.1080/01621459.1963.10500830 Google Scholar
[15] Kahane, J.-P., Some random series of functions. 2nd edition. Cambridge, Cambridge University Press, 1985.Google Scholar
[16] Kaufman, R., On the theorem ofjarnik and Besicovitch. Acta Arith. 39(1981), no. 3, 265–267.Google Scholar
[17] Körner, T. W., On the theorem of Ivasev-Musatov. III. Proc. London Math. Soc. (3) 53(1986), no. 1,143–192. http://dx.doi.Org/10.1112/plms/s3-53.1.143 Google Scholar
[18] Körner, T. W., On a theorem ofSaeki concerning convolution squares of singular measures. Bull. Soc. Math. France 136(2008), 439–464.Google Scholar
[19] Körner, T. W.,Baire category, probabilistic constructions and convolution squares. Lecture notes, University of Cambridge, 2009.Google Scholar
[20] Körner, T. W., Hausdorff and Fourier dimension. Studia Math. 206 (2011), no. 1, 37–50.http://dx.doi.org/10.4064/sm206-1-3 Google Scholar
[21] łaba, I., Harmonic analysis and the geometry of fractals, Proceedings of the 2014 International Congress of Mathematicians, to appear.Google Scholar
[22] łaba, I. and Pramanik, M., Arithmetic progressions in sets of fractional dimension. Geom. Funct.Anal. 19(2009), no. 2, 429–456.http://dx.doi.Org/10.1007/s00039-009-0003-9 Google Scholar
[23] Mattila, P., Hausdorff dimension, projections, and the Fourier transform. Publ. Mat. 48(2004), no. 1, 3–48. http://dx.doi.org/10.5565/PUBLMAT_48104_01 Google Scholar
[24] Mitsis, T., Stein-Tomas, A restriction theorem for general measures. Publ. Math. Debrecen 60(2002), no. 1-2, 89–99.Google Scholar
[25] Mockenhaupt, G., Salem sets and restriction properties of Fourier transform. Geom. Funct. Anal. 10(2000), no. 6, 1579–1587. http://dx.doi.org/10.1007/PL00001662 Google Scholar
[26] Rudin, W., Trigonometric series with gaps. J. Math. Mech. 9(1960), 203–227.Google Scholar
[27] Saeki, S., On convolution powers of singular measures. Illinois J. Math. 24(1980), 225–232.Google Scholar
[28] Salem, R.,On singular monotonie functions whose spectrum has a given Hausdorff dimension. Ark.Mat. 1(1951), no. 4, 353–365. http://dx.doi.org/10.1007/BF02591372 Google Scholar
[29] Senthil Raani, K. S., Lp asymptotics of Fourier transform of fractal measures. Ph.D. Thesis, Indian Institute of Science, Bangalore, 2015.Google Scholar
[30] Shmerkin, P. and Suomala, V., Spatially independent martingales, intersections, and applications. Memoirs of the American Mathematical Society, to appear. arxiv:1409.6707.Google Scholar
[31] Stein, E. M. and Shakarchi, R., Functional analysis. Princeton, Princeton University Press, 2011.Google Scholar
[32] Strichartz, R., Fourier asymptotics of fractal measures. J. Funct. Anal. 89(1990), no. 1,154–187.http://dx.doi.Org/10.1016/0022-1236(90)90009-A Google Scholar
[33] Tao, T., Some recent progress on the restriction conjecture. Fourier analysis and convexity. Appl. Numer. Harmon. Anal., Birkhäuser, Boston, MA, 2004. pp. 217–243.Google Scholar
[34] Tomas, P. A., A restriction theorem for the Fourier transform. Bull. Amer. Math. Soc. 81(1975), 477–478. http://dx.doi.org/10.1090/S0002-9904-1975-13790-6 Google Scholar
[35] Tomas, P. A., Restriction theorems for the Fourier transform. In: Harmonic analysis in Euclidean spaces. Proc. Symp. Pure Math. American Mathematical Society, Providence, RI, 1979,pp. 111–114.Google Scholar
[36] Wiener, N. and Wintner, A., Fourier-Stieltjes transforms and singular infinite convolutions. Amer. J. Math 60(1938), 513–522.http://dx.doi.org/10.2307/2371591 Google Scholar
[37] Wolff, T. H., Lectures on harmonic analysis. I. ł aba and C. Shubin, eds. University Lecture Series 29. American Mathematical Society, Providence, RI, 2003.Google Scholar