Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jordan, J. H.
and
Schneider, D. G.
1971.
Covering Classes of Residues in Z(√–2).
Mathematics Magazine,
Vol. 44,
Issue. 5,
p.
257.
Friedlander, John
1972.
On exact coverings of the integers.
Israel Journal of Mathematics,
Vol. 12,
Issue. 3,
p.
299.
Silverman, Joseph H.
1978.
Mean and Variance for Covering Sets of Congruences.
Mathematics Magazine,
Vol. 51,
Issue. 2,
p.
120.
Guy, Richard K.
1981.
Unsolved Problems in Number Theory.
p.
132.
Guy, Richard K.
1994.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
240.
Guy, Richard K.
2004.
Unsolved Problems in Number Theory.
Vol. 1,
Issue. ,
p.
365.

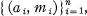 with
with 