Article contents
Coxeter Diagrams and the Köthe’s Problem
Published online by Cambridge University Press: 24 February 2020
Abstract
A ring 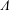 $\unicode[STIX]{x1D6EC}$ is called right Köthe if every right
$\unicode[STIX]{x1D6EC}$ is called right Köthe if every right 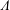 $\unicode[STIX]{x1D6EC}$-module is a direct sum of cyclic modules. In this paper, we give a characterization of basic hereditary right Köthe rings in terms of their Coxeter valued quivers. We also give a characterization of basic right Köthe rings with radical square zero. Therefore, we give a solution to Köthe’s problem in these two cases.
$\unicode[STIX]{x1D6EC}$-module is a direct sum of cyclic modules. In this paper, we give a characterization of basic hereditary right Köthe rings in terms of their Coxeter valued quivers. We also give a characterization of basic right Köthe rings with radical square zero. Therefore, we give a solution to Köthe’s problem in these two cases.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The research of the first author was in part supported by a grant from IPM. Also, the research of the second author was in part supported by a grant from IPM (No. 98170412).
References
- 3
- Cited by



