Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T12:16:13.906Z Has data issue: false hasContentIssue false
  • English
  • Français

A CR Analogue of Yau’s Conjecture on Pseudoharmonic Functions of Polynomial Growth

Part of: Global differential geometry CR manifolds

Published online by Cambridge University Press:  07 January 2019

Der-Chen Chang ,
Shu-Cheng Chang ,
Yingbo Han  and
Jingzhi Tie
Der-Chen Chang
Affiliation:
Department of Mathematics and Statistics, Georgetown University, Washington DC, 20057-0001, USA Department of Mathematics, Fu Jen Catholic University, Taipei 242, Taiwan, R.O.C. Email: chang@georgetown.edu
Shu-Cheng Chang
Affiliation:
Department of Mathematics and Taida Institute for Mathematical Sciences (TIMS), National Taiwan University, Taipei 10617, Taiwan Email: scchang@math.ntu.edu.tw
Yingbo Han
Affiliation:
School of Mathematics and Statistics, Xinyang Normal University, Xinyang, 464000, Henan, P.R. China Email: yingbohan@163.com
Jingzhi Tie
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA, 30602-7403, USA Email: jtie@math.uga.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we first derive the CR volume doubling property, CR Sobolev inequality, and the mean value inequality. We then apply them to prove the CR analogue of Yau’s conjecture on the space consisting of all pseudoharmonic functions of polynomial growth of degree at most 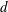$d$ in a complete noncompact pseudohermitian 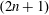$(2n+1)$-manifold. As a by-product, we obtain the CR analogue of the volume growth estimate and the Gromov precompactness theorem.

Keywords

CR Bochner formulaheat kernelsubgradient estimateLiouvile theoremCR volume doubling propertyCR Sobolev inequalitymean value inequality

MSC classification

Primary: 32V05: CR structures, CR operators, and generalizations
Secondary: 32V20: Analysis on CR manifolds 53C56: Other complex differential geometry
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1367 - 1394
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author D.-C. C. is partially supported by an NSF grant DMS-1408839 and a McDevitt Endowment Fund at Georgetown University. Author S.-C. C. is partially supported by the MOST of Taiwan. (Corresponding author) Y. H. is partially supported by an NSFC grant 11201400, Nanhu Scholars Program for Young Scholars of Xinyang Normal University and the Universities Young Teachers Program of Henan Province (2016GGJS-096).

References

Bakry, D. and Emery, M., Diffusions hypercontractives. In: Séminaire de probabilité, XIX. Lecture Notes in Math., 1123. Springer, Berlin, 1985, pp. 177–206. https://doi.org/10.1007/BFb0075847.Google Scholar
Baudoin, F., Bonnefont, M., and Garofalo, N., A sub-Riemannian curvature-dimension inequality, volume doubling property and the Poincaré inequality . Math. Ann. 358(2014), no. 3–4, 833–860. https://doi.org/10.1007/s00208-013-0961-y.Google Scholar
Baudoin, F., Bonnefont, M., Garofalo, N., and Munive, I., Volume and distance comparison theorems for sub-Riemannian manifolds . J. Funct. Anal. 267(2014), no. 7, 2005–2027. https://doi.org/10.1016/j.jfa.2014.07.030.Google Scholar
Beals, R. and Greiner, P. C., Calculus on Heisenberg manifolds . Annals of Mathematics Studies, 119. Princeton University Press, Princeton, NJ, 1988. https://doi.org/10.1515/9781400882397.Google Scholar
Beals, R., Gaveau, B., and Greiner, P. C., Hamilton-Jacobi theory and the heat kernel on Heisenberg groups . J. Math Pures Appl. 79(2000), 633–689. https://doi.org/10.1016/S0021-7824(00)00169-0.Google Scholar
Beardon, A. F., Sums of powers of integers . Amer. Math. Monthly 103(1996), no. 3, 201–213. https://doi.org/10.2307/2975368.Google Scholar
Berenstein, C., Chang, D.-C., and Tie, J., Laguerre calculus and its application on the Heisenberg group . AMS/IP Studies in Advanced Mathematics, 22. American Mathematical Society, Providence, RI and International Press, CambridgeSomerville, MA, 2001.Google Scholar
Calin, O., Chang, D.-C., Furutani, K., and Iwasaki, C., Heat kernels for elliptic and sub-elliptic operators: methods and techniques . Birkhäuser-Springer, New York, 2011. https://doi.org/10.1007/978-0-8176-4995-1.Google Scholar
Calin, O., Chang, D.-C., and Tie, J., Fundamental solutions for Hermite and subelliptic operators . J. Anal. Math. 100(2006), 223–248. https://doi.org/10.1007/BF02916762.Google Scholar
Cao, H.-D. and Yau, S.-T., Gradient estimate, Harnack inequalities and estimates for Heat kernel of the sum of squares of vector fields . Math. Z. 221(1992), 485–504. https://doi.org/10.1007/BF02571441.Google Scholar
Chang, D.-C., Chang, S.-C., and Lin, C., On Li-Yau gradient estimate for sum of squares of vector fields up to higher step. To appear in: Comm. Anal. Geom. arxiv:1602.01531 https://doi.org/10.1007/BF02571441.Google Scholar
Chang, S.-C., Kuo, T.-J., and Lai, S.-H., Li-Yau gradient estimate and entropy formulae for the CR heat equation in a closed pseudohermitian 3-manifold . J. Differential Geom. 89(2011), 185–216. https://doi.org/10.4310/jdg/1324477409.Google Scholar
Chang, S.-C., Kuo, T.-J., Lin, C., and Tie, J., CR sub-Laplacian comparison and Liouville-type theorem in a complete noncompact Sasakian manifold. arxiv:1506.03270.Google Scholar
Chang, S.-C., Tie, J., and Wu, C.-T., Subgradient estimate and Liouville-type theorem for the CR heat equation on Heisenberg groups . Asian J. Math. 14(2010), no. 1, 41–72. https://doi.org/10.4310/AJM.2010.v14.n1.a4.Google Scholar
Cheeger, J., Colding, T. H., and Minicozzi, W. P., Linear growth harmonic functions on complete manifolds with nonnegative Ricci curvature . Geom. Funct. Anal. 5(1995), no. 6, 948–954. https://doi.org/10.1007/BF01902216.Google Scholar
Cheng, S.-Y. and Yau, S.-T., Differential equations on Riemannian manifolds and their geometric applications . Comm. Pure Appl. Math. 28(1975), 333–354. https://doi.org/10.1002/cpa.3160280303.Google Scholar
Chow, W.-L., Uber system von lineaaren partiellen Differentialgleichungen erster Orduung . Math. Ann. 117(1939), 98–105. https://doi.org/10.1007/BF01450011.Google Scholar
Cohn, W. S. and Lu, G., Best constants for Moser-Trudinger inequalities on the Heisenberg group . Indiana Univ. Math. J. 50(2001), 1567–1591. https://doi.org/10.1512/iumj.2001.50.2138.Google Scholar
Colding, T. H. and Minicozzi, W. P., Harmonic functions on manifolds . Ann. of Math. 146(1997), no. 3, 725–747. https://doi.org/10.2307/2952459.Google Scholar
Dragomir, S. and Tomassini, G., Differential geometry and analysis on CR manifolds . Progress in Mathematics, 246. Birkhäuser Boston, Boston, MA, 2006.Google Scholar
Dunkl, C. F., An addition theorem for Heisenberg harmonics . In: Conference on Harmonic Analysis in Honor of Antoni Zygmund, Wadsworth International, Belmont, CA , 1983, pp. 690–707.Google Scholar
Folland, G. B. and Stein, E. M., Estimates for the ∂̄b complex and analysis on the Heisenberg group . Comm. Pure Appl. Math. 27(1974), 429–522. https://doi.org/10.1002/cpa.3160270403.Google Scholar
Gaveau, B., Principe de moindre action, propagation de la chaleur et estimées sous elliptiques sur certains groupes nilpotents . Acta Math. 139(1977), 95–153. https://doi.org/10.1007/BF02392235.Google Scholar
Greenleaf, A., The first eigenvalue of a sub-Laplacian on a pseudo-Hermitian manifold . Comm. Partial Differential Equations 10(1985), no. 3, 191–217. https://doi.org/10.1080/03605308508820376.Google Scholar
Greiner, P. C., Spherical harmonics on the Heisenberg group . Canad. Math. Bull. 23(1980), 383–396. https://doi.org/10.4153/CMB-1980-057-9.Google Scholar
Gromov, M., Metric structures for Riemannian and non-Riemannian spaces . Progress in Mathematics, 152. Birkhäuser Boston, Boston, MA, 1999.Google Scholar
Hulanicki, A., The distribution of energy in the Brownian motion in the Gaussian field and analytic-hypoellipticity of certain subelliptic operators on the Heisenberg group . Studia Math. 56(1976), 165–173. https://doi.org/10.4064/sm-56-2-165-173.Google Scholar
Kasue, A., Harmonic functions with growth conditions on a manifold of asymptotically nonnegative curvature II . In: Recent topics in differential and analytic geometry . Adv. Stud. Pure Math., 18. Academic Press, Boston, MA, 1990, pp. 283–301.Google Scholar
Korányi, A. and Stanton, N., Liouville-type theorems for some complex hypoelliptic operators . J. Funct. Anal. 60(1985), 370–377. https://doi.org/10.1016/0022-1236(85)90045-X.Google Scholar
Lee, J. M., Pseudo-Einstein structure on CR manifolds . Amer. J. Math. 110(1988), 157–178. https://doi.org/10.2307/2374543.Google Scholar
Li, P., Geometric analysis . Cambridge Studies in Advanced Mathematics, 134. Cambridge University Press, Cambridge, 2012. https://doi.org/10.1017/CBO9781139105798.Google Scholar
Li, P., Harmonic functions on Kähler manifolds with nonnegative Ricci curvature . Math. Res. Lett. 2(1995), 79–94. https://doi.org/10.4310/MRL.1995.v2.n1.a8.Google Scholar
Li, P., Harmonic sections of polynomial growth . Math. Res. Lett. 4(1997), 35–44. https://doi.org/10.4310/MRL.1997.v4.n1.a4.Google Scholar
Li, P. and Tam, L.-F., Linear growth harmonic functions on a complete manifold . J. Differential Geom. 29(1989), 421–425. https://doi.org/10.4310/jdg/1214442883.Google Scholar
Li, P. and Tam, L.-F., Complete surfaces with finite total curvature . J. Differential Geom. 33(1991), 139–168. https://doi.org/10.4310/jdg/1214446033.Google Scholar
Li, P. and Yau, S.-T., On the parabolic kernel of the Schrödinger operator . Acta Math. 156(1985), 153–201. https://doi.org/10.1007/BF02399203.Google Scholar
Liu, G., On the volume growth of Kähler manifolds with nonnegative bisectional curvature . J. Differential Geom. 102(2016), no. 3, 485–500. https://doi.org/10.4310/jdg/1456754016.Google Scholar
Nagel, A., Analysis and geometry on Carnot-Carathéodory spaces. http://www.math.wisc.edu/∼nagel/2005Book.pdf.Google Scholar
Saloff-Coste, L., Uniformly elliptic operators on Riemannian manifolds . J. Differential Geom. 36(1992), 417–450. https://doi.org/10.4310/jdg/1214448748.Google Scholar
Saloff-Coste, L., Aspect of Sobolev-type inequalities . London Mathematical Society Lecture Notes Series, 289. Cambridge University Press, Cambridge, 2002.Google Scholar
Siu, Y.-T. and Yau, S.-T., Complete Kähler manifolds with non-positive curvature of faster than quadratic decay . Ann. of Math. 105(1977), 225–264. https://doi.org/10.2307/1970998.Google Scholar
Villani, C., Optimal transport. Old and new . Grundlehren der Mathematischen Wissenschaften, 338. Springer-Verlag, Berlin, 2009. https://doi.org/10.1007/978-3-540-71050-9.Google Scholar
Xu, G., Three circles theorems for harmonic functions . Math. Ann. 366(2016), 1281–1317. https://doi.org/10.1007/s00208-016-1366-5.Google Scholar
Yau, S.-T., Harmonic functions on complete Riemannian manifolds . Comm. Pure Appl. Math. 28(1975), 201–228. https://doi.org/10.1002/cpa.3160280203.Google Scholar
Yau, S.-T., Open problems in geometry. In: Lectures on differential geometry, International Press, 1994, pp. 365–404.Google Scholar
S.-T. Yau, ed. Seminar on differential geometry. Annals of Mathematics Studies, 102. Princeton University Press, Princeton, NJ, 1982.Google Scholar