Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T23:34:36.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical Points and Resonance of Hyperplane Arrangements

Published online by Cambridge University Press:  20 November 2018

D. Cohen ,
G. Denham ,
M. Falk  and
A. Varchenko
D. Cohen
Affiliation:
Department of Mathematics, Louisiana State University, Baton Rouge, LA 70803, U.S.A. email: cohen@math.lsu.edu
G. Denham
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7 email: gdenham@uwo.ca
M. Falk
Affiliation:
Department of Mathematics and Statistics, Northern Arizona University, Flagstaff, AZ 86011, U.S.A. email: michael.falk@nau.edu
A. Varchenko
Affiliation:
Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, U.S.A. email: anv@email.unc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

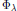If ${{\Phi }_{\lambda }}$ is a master function corresponding to a hyperplane arrangement 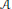$\mathcal{A}$ and a collection of weights 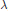$\lambda $, we investigate the relationship between the critical set of 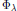${{\Phi }_{\lambda }}$, the variety defined by the vanishing of the one-form 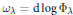${{\omega }_{\lambda }}=\text{d}\log {{\Phi }_{\lambda }}$, and the resonance of 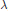$\lambda $. For arrangements satisfying certain conditions, we show that if 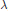$\lambda $ is resonant in dimension 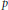$p$, then the critical set of 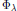${{\Phi }_{\lambda }}$ has codimension at most 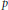$p$. These include all free arrangements and all rank 3 arrangements.

Keywords

32S2255N2552C35hyperplane arrangementmaster functionresonant weightscritical set
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 5 , 18 October 2011 , pp. 1038 - 1057
Copyright
Copyright © Canadian Mathematical Society 2011

References

[Coh02] Cohen, D., Triples of arrangements and local systems. Proc. Amer. Math. Soc. 130(2002), no. 10, 3025–3031. doi:10.1090/S0002-9939-02-06428-6Google Scholar
[CV03] Cohen, D. and A. N. Varchenko, Resonant local systems on complements of discriminantal arrangements and sl 2 representations. Geom. Dedicata 101(2003), 217–233. doi:10.1023/A:1026370732724Google Scholar
[Dam99] Damon, J., Critical points of affine multiforms on the complements of arrangements. In: Singularity theory (Liverpool, 1996), London Math. Soc. Lecture Note Ser., 263, Cambridge University Press, Cambridge, 1999, pp. 25–53.Google Scholar
[Den07] Denham, G., Zeroes of 1-forms and resonance of free arrangements, Oberwolfach Rep. 4 (2007), no. 3, 2345–2347.Google Scholar
[Dim08] Dimca, A., Characteristic varieties and logarithmic differential 1-forms. Compos. Math. 146(2010), no. 1, 129–144. doi:10.1112/S0010437X09004461Google Scholar
[Eis95] Eisenbud, D., Commutative algebra. With a view toward algebraic geometry. Graduate Texts in Mathematics, 150, Springer-Verlag, New York, 1995.Google Scholar
[ESV92] Esnault, H., V. Schechtman, and V. Viehweg, Cohomology of local systems on the complement of hyperplanes. Invent. Math. 109(1992), no. 3, 557–561. Erratum, ibid., 112(1993), no. 2, 447. doi:10.1007/BF01232040Google Scholar
[Fal07] Falk, M., Resonance and zeros of logarithmic one-forms with hyperplane poles, Oberwolfach Rep. 4 (2007), no. 3, 2343–2345.Google Scholar
[FY07] Falk, M. and S. Yuzvinsky, Multinets, resonance varieties, and pencils of plane curves. Compos. Math. 143(2007), no. 4, 1069–1088.Google Scholar
[Far01] Farber, M., Topology of closed 1-forms and their critical points. Topology 40(2001), no. 2, 235–258. doi:10.1016/S0040-9383(99)00059-2Google Scholar
[Far04] Farber, M., Topology of closed one-forms. Mathematical Surveys and Monographs, 108, American Mathematical Society, Providence, RI, 2004.Google Scholar
[GS] Grayson, D. and M. Stillman, Macaulay 2: a software system for research in algebraic geometry. http://www.math.uiuc.edu/Macaulay2.Google Scholar
[HKS05] Ho, S.şten, A. Khetan, and B. Sturmfels, Solving the likelihood equations. Found. Comput. Math. 5(2005), no. 4, 389–407. doi:10.1007/s10208-004-0156-8Google Scholar
[MV04] Mukhin, E. and A. Varchenko, Critical points of master functions and flag varieties. Commun. Contemp. Math. 6(2004), no. 1, 111–163. doi:10.1142/S0219199704001288Google Scholar
[MV05] Mukhin, E. and A. Varchenko, Miura opers and critical points of master functions. Cent. Eur. J. Math. 3(2005), no. 2, 155–182 (electronic). doi:10.2478/BF02479193Google Scholar
[MS01] Musta, M.ţă and H. Schenck, The module of logarithmic p-forms of a locally free arrangement. J. Algebra 241(2001), no. 2, 699–719. doi:10.1006/jabr.2000.8606Google Scholar
[OS02] Orlik, P. and R. Silvotti, Local system homology of arrangement complements. In: Arrangements—Tokyo 1998, Adv. Stud. Pure Math., 27, Kinokuniya, Tokyo, 2000, pp. 247–256.Google Scholar
[OT92] Orlik, P. and H. Terao, Arrangements of hyperplanes. Grundlehren Mathematischen Wissenschaften, 300, Springer-Verlag, Berlin, 1992.Google Scholar
[OT95a] Orlik, P. and H. Terao, The number of critical points of a product of powers of linear functions. Invent. Math. 120(1995), no. 1, 1–14. doi:10.1007/BF01241120Google Scholar
[OT95b] Orlik, P. and H. Terao, Arrangements and Milnor fibers. Math. Ann. 301(1995), no. 2, 211–235. doi:10.1007/BF01446627Google Scholar
[OT01] Orlik, P. and H. Terao, Arrangements and hypergeometric integrals. MSJ Memoirs, 9, Mathematical Society of Japan, Tokyo, 2001.Google Scholar
[RV95] Reshetikhin, N. and A. Varchenko, Quasiclassical asymptotics of solutions to the KZ equations. In: Geometry, topology, and physics, Conf. Proc. Lecture Notes Geom. Topology, IV, Int. Press, Cambridge, MA, 1995, pp. 293–322.Google Scholar
[STV95] Schechtman, V., H. Terao, and A. Varchenko, Local systems over complements of hyperplanes and the Kac-Kazhdan conditions for singular vectors. J. Pure Appl. Algebra 100(1995), no. 1–3, 93–102. doi:10.1016/0022-4049(95)00014-NGoogle Scholar
[SV91] Schechtman, V. and A. Varchenko, Arrangements of hyperplanes and Lie algebra homology. Invent. Math. 106(1991), no. 1, 139–194. doi:10.1007/BF01243909Google Scholar
[SV03] Scherbak, I. and A. Varchenko, Critical points of functions, sl representations, and Fuchsian differential equations with only univalued solutions. Mosc. Math. J. 3(2003), no. 2, 621–645, 745. 2Google Scholar
[Sil96] Silvotti, R., On a conjecture of Varchenko. Invent. Math. 126(1996), no. 2, 235–248. doi:10.1007/s002220050096Google Scholar
[Suc02] I, A.. Suciu, Translated tori in the characteristic varieties of complex hyperplane arrangements. Topology Appl. 118(2002), no. 1–2, 209–223. doi:10.1016/S0166-8641(01)00052-9Google Scholar
[TY95] Terao, H. and S. Yuzvinsky, Logarithmic forms on affine arrangements. Nagoya Math. J. 139(1995), 129–149.Google Scholar
[Var95] Varchenko, A., Critical points of the product of powers of linear functions and families of bases of singular vectors. Compositio Math. 97(1995), no. 3, 385–401.Google Scholar
[Var06] Varchenko, A., Bethe ansatz for arrangements of hyperplanes and the Gaudin model. Mosc. Math. J. 6(2006), no. 1, 195–210, 223–224.Google Scholar
[WY97] Wiens, J. and S. Yuzvinsky, De Rham cohomology of logarithmic forms on arrangements of hyperplanes. Trans. Amer. Math. Soc. 349(1997), no. 4, 1653–1662. doi:10.1090/S0002-9947-97-01894-1Google Scholar
[Yuz95] Yuzvinsky, S., Cohomology of the Brieskorn-Orlik-Solomon algebras. Comm. Algebra 23(1995), no. 14, 5339–5354. doi:10.1080/00927879508825535Google Scholar
[Suc02] I, A.. Suciu, Translated tori in the characteristic varieties of complex hyperplane arrangements. Topology Appl. 118(2002), no. 1–2, 209–223. doi:10.1016/S0166-8641(01)00052-9Google Scholar
[TY95] Terao, H. and S. Yuzvinsky, Logarithmic forms on affine arrangements. Nagoya Math. J. 139(1995), 129–149.Google Scholar
[Var95] Varchenko, A., Critical points of the product of powers of linear functions and families of bases of singular vectors. Compositio Math. 97(1995), no. 3, 385–401.Google Scholar
[Var06] Varchenko, A., Bethe ansatz for arrangements of hyperplanes and the Gaudin model. Mosc. Math. J. 6(2006), no. 1, 195–210, 223–224.Google Scholar
[WY97] Wiens, J. and S. Yuzvinsky, De Rham cohomology of logarithmic forms on arrangements of hyperplanes. Trans. Amer. Math. Soc. 349(1997), no. 4, 1653–1662. doi:10.1090/S0002-9947-97-01894-1Google Scholar
[Yuz95] Yuzvinsky, S., Cohomology of the Brieskorn-Orlik-Solomon algebras. Comm. Algebra 23(1995), no. 14, 5339–5354. doi:10.1080/00927879508825535Google Scholar