No CrossRef data available.
Article contents
Cubic Polynomials with Periodic Cycles of a Specified Multiplier
Published online by Cambridge University Press: 20 November 2018
Abstract
We consider cubic polynomials 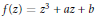 $f\left( z \right)\,=\,{{z}^{3}}\,+\,az\,+\,b$ defined over
$f\left( z \right)\,=\,{{z}^{3}}\,+\,az\,+\,b$ defined over 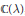 $\mathbb{C}\left( \lambda \right)$, with a marked point of period
$\mathbb{C}\left( \lambda \right)$, with a marked point of period 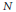 $N$ and multiplier
$N$ and multiplier 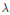 $\lambda$. In the case
$\lambda$. In the case 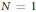 $N\,=\,1$, there are infinitely many such objects, and in the case
$N\,=\,1$, there are infinitely many such objects, and in the case 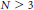 $N\,\ge \,3$, only finitely many (subject to a mild assumption). The case
$N\,\ge \,3$, only finitely many (subject to a mild assumption). The case 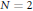 $N\,=\,2$ has particularly rich structure, and we are able to describe all such cubic polynomials defined over the field
$N\,=\,2$ has particularly rich structure, and we are able to describe all such cubic polynomials defined over the field 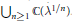 ${{\cup }_{n\ge 1}}\,\mathbb{C}\left( {{\lambda }^{1/n}} \right)$.
${{\cup }_{n\ge 1}}\,\mathbb{C}\left( {{\lambda }^{1/n}} \right)$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2012


