Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boutellier, Roman
1981.
Curvature and functions with bounded boundary rotation.
Mathematische Zeitschrift,
Vol. 177,
Issue. 3,
p.
395.


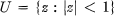 and having the representation
and having the representation