No CrossRef data available.
Article contents
Cyclic Groups and the Three Distance Theorem
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We give a two dimensional extension of the three distance theorem. Let 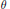 $\theta $ be in
$\theta $ be in 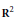 ${{\mathbf{R}}^{2}}$ and let
${{\mathbf{R}}^{2}}$ and let  $q$ be in
$q$ be in 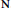 $\mathbf{N}$ . There exists a triangulation of
$\mathbf{N}$ . There exists a triangulation of 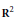 ${{\mathbf{R}}^{2}}$ invariant by
${{\mathbf{R}}^{2}}$ invariant by 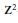 ${{\mathbf{Z}}^{2}}$ -translations, whose set of vertices is
${{\mathbf{Z}}^{2}}$ -translations, whose set of vertices is 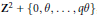 ${{\mathbf{Z}}^{2}}\,+\,\{0,\,\theta ,\,\ldots ,\,q\theta \}$ , and whose number of different triangles, up to translations, is bounded above by a constant which does not depend on
${{\mathbf{Z}}^{2}}\,+\,\{0,\,\theta ,\,\ldots ,\,q\theta \}$ , and whose number of different triangles, up to translations, is bounded above by a constant which does not depend on 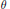 $\theta $ and
$\theta $ and  $q$ .
$q$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
[1]
Allessandri, P. and Berthé, V., Three distance theorems and combinatorics on words. Enseign. Math
44(1998), no. 1-2, 103–132.Google Scholar
[2]
Babai, L., On Lovász’ lattice reduction and the nearest lattice point problem. Combinatorica
6(1986), no. 1, 1–13.Google Scholar
[3]
Berthé, V. and Tijdeman, R., Balance properties of multi-dimensional words. Theoret. Comput. Sci.
273(2002), no. 1-2, 197–224.Google Scholar
[4]
Boot, B., Okabe, A., and Sugihara, K., Spatial Tessellations, Concepts and Applications of Voronoï Diagrams.
John Wiley, 1991.Google Scholar
[5]
Chevallier, N., Meilleures approximations d’un élément du tore T2
et géométrie de la suite des multiples de cet élément.
Acta Arith.
78(1996), no. 1, 19–35.Google Scholar
[6]
Chevallier, N., Géométrie des suites de Kronecker. Manuscripta Math.
94(1997), no. 2, 231–241.Google Scholar
[7]
Chevallier, N., Three distance theorem and grid graph. Discrete Math.
223(2000), no. 1-3, 355–362.Google Scholar
[8]
Chevallier, N., Meilleures approximations diophantiennes d’un élément du tore T
d.
Acta Arith.
97(2001), no. 3, 219–240.Google Scholar
[9]
Chung, F. R. K. and Graham, R. L., On the set of distances determined by union of arithmetic progression. Ars. Combinatoria
1(1976), no. 1, 57–76.Google Scholar
[10]
Dieudonné, J., Éléments d’analyse. I. fondements de l’analyse moderne.
Gauthier-Villars, Paris, 1972.Google Scholar
[11]
Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications.
Lectures Notes in Mathematics
1651, Springer-Verlag, Berlin, 1997.Google Scholar
[12]
Fried, E. and Sós, V. T., A generalization of the three-distance theorem for groups. Algebra Universalis,
29(1992), no. 1, 136–149.Google Scholar
[13]
Grötschel, M., Lovász, L., and Schrijver, A., Geometric Algorithms and Combinatorial Optimization. Second edition. Algorithms and Combinatorics 2, Springer-Verlag, Berlin, 1993.Google Scholar
[14]
Geelen, A. S. and Simpson, R. J., A two dimensional Steinhaus theorem.
Australas. J. Combin. 8 (1993), 136–197.Google Scholar
[15]
Lagarias, J. C., Some new results in simultaneous Diophantine approximation.
Proc. of the Queen's Number Theory Conference 1979 (Ribenboim, P., Ed.), Queen's Paper in Pure and Applied Math. No. 54 (1980), 453–474.Google Scholar
[16]
Lagarias, J. C., Best simultaneous Diophantine approximations I. Growth Rates of Best Approximations denominators, Trans. Amer. Math. Soc.
272(1982), no. 2, 545–554.Google Scholar
[17]
Lagarias, J. C., Best simultaneous Diophantine approximations II. Behavior of consecutive best approximations. Pacific J. Math.
102(1982), no. 1, 61–88.Google Scholar
[18]
Lagarias, J. C., Best Diophantine approximations to a set of linear forms. J. Austral. Math. Soc. Ser. A
34(1983), no. 1, 114–122.Google Scholar
[19]
Lagarias, J. C., The computational complexity of simultaneous Diophantine approximations problems. SIAM J. Comput.
14(1985), no. 1, 196–209.Google Scholar
[20]
Lagarias, J. C., Geodesic multidimensional continued fractions. Proc. London Math. Soc.
69(1994), no. 3, 464–488.Google Scholar
[21]
Langevin, M., Stimulateur cardiaque et suite de Farey. Period. Math. Hungar.
23(1991), no. 1, 75–86.Google Scholar
[22]
Liang, F. M., A short proof of the 3d distance theorem.
Discrete Math.
28 (1979), no. 3, 325–326.Google Scholar
[23]
Mignosi, F., On the number of factors of Sturmian words. Theoret. Comput. Sci.
82(1991), no. 1, 71–84.Google Scholar
[24]
Preparata, F. P. and Shamos, M. I., Computational geometry. An Introduction.
Texts and Monographs in Computer Science, Springer-Verlag, New York, 1985.Google Scholar
[25]
Pytheas Fogg, N., Substitutions in Dynamics, Arithmetic and Combinatorics.
Lectures Notes in Mathematics
1794, Springer-Verlag, Berlin, 2002.Google Scholar
[26]
van Ravenstein, T., Three gap theorem (Steinhaus conjecture). J. Austral. Math. Soc. Ser. a
45(1988), no. 3, 360–370.Google Scholar
[27]
Rogers, C. A., The signatures of the errors of some simultaneous Diophantine approximations. Proc. London Math. Soc.
52(1951), 186–190.Google Scholar
[28]
Siegel, A., Théorème des trois longueurs et suites sturmiennes: mots d’agencement des longueurs. Acta Arith.
97(2001), no. 3, 195–210.Google Scholar
[29]
Slater, N. B., The distribution of the integers N for whic. ﹛θN﹜ < ϕ. Proc. Cambridge Philos. Soc.
46(1950), 525–534.Google Scholar
[30]
Slater, N. B., Distribution problems and physical applications. Compositio Math.
16(1964), 176–183.Google Scholar
[31]
Slater, N. B., Gaps and steps for the sequence nθ. mod 1. Proc. Cambridge Philos. Soc.
63(1967), 1115–1123.Google Scholar
[32]
Sós, V. T., On the theory of diophantine approximation. I. Acta Math. Acad. Sci. Hung.
8(1957), 461–472.Google Scholar
[33]
Sós, V. T., On the theory of Diophantine approximation. II. Acta Math. Acad. Sci. Hung.
9(1958), 229–241.Google Scholar
[34]
Sós, V. T., On the distribution mod 1 of the sequence nα, Ann. Univ. Sci. Budapest, Eötvös Sect. Math.
1 (1958), 127–134.Google Scholar
[35]
Świerczkowski, S., On the successive settings of an arc on the circumference of a circle. Fund. Math.
46(1959), 187–189.Google Scholar

