Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:12:43.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposability of von Neumann Algebras and the Mazur Property of Higher Level

Published online by Cambridge University Press:  20 November 2018

Zhiguo Hu  and
Matthias Neufang
Zhiguo Hu
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON, N9B 3P4 e-mail: zhiguohu@uwindsor.ca
Matthias Neufang
Affiliation:
School of Mathematics and Statistics, Carleton University, Ottawa, ON, K1S 5B6 e-mail: mneufang@math.carleton.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The decomposability number of a von Neumann algebra 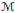$\mathcal{M}$ (denoted by 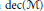$\text{dec}\left( \mathcal{M} \right)$) is the greatest cardinality of a family of pairwise orthogonal non-zero projections in 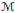$\mathcal{M}$. In this paper, we explore the close connection between 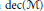$\text{dec}\left( \mathcal{M} \right)$ and the cardinal level of the Mazur property for the predual 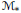${{\mathcal{M}}_{*}}$ of 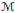$\mathcal{M}$, the study of which was initiated by the second author. Here, our main focus is on those von Neumann algebras whose preduals constitute such important Banach algebras on a locally compact group 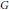$G$ as the group algebra 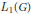${{L}_{1}}(G)$, the Fourier algebra 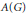$A(G)$, the measure algebra 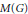$M(G)$, the algebra 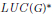$LUC{{(G)}^{*}}$, etc. We show that for any of these von Neumann algebras, say 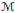$\mathcal{M}$, the cardinal number dec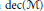$(\mathcal{M})$ and a certain cardinal level of the Mazur property of 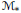${{\mathcal{M}}_{*}}$ are completely encoded in the underlying group structure. In fact, they can be expressed precisely by two dual cardinal invariants of 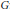$G$: the compact covering number 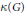$\kappa (G)$ of 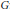$G$ and the least cardinality 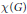$\mathcal{X}(G)$ of an open basis at the identity of 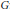$G$. We also present an application of the Mazur property of higher level to the topological centre problem for the Banach algebra 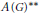$A{{(G)}^{**}}$.

Keywords

22D0543A2043A3003E5546L10Mazur propertypredual of a von Neumann algebralocally compact group and its cardinal invariantsgroup algebraFourier algebratopological centre
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 4 , 01 August 2006 , pp. 768 - 795
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Akemann, C. A. and Anderson, J., Lyapunov Theorems for Operator Algebras. Mem. Amer. Math. Soc. 94(1991), no. 458.Google Scholar
[2] Berglund, J. F., Junghenn, H. D. and Milnes, P. Analysis on Semigroups: Function Spaces, Compactification, Representations. Wiley, New York, 1989.Google Scholar
[3] Chou, C., Topological invariant means on the von Neumann algebr VN(G). Trans. Amer. Math. Soc. 273(1982), no. 1, 207–229.Google Scholar
[4] Chu, C. H., von Neumann algebras which are second dual spaces. Proc. Amer. Math. Soc. 112(1991), no. 4, 999–1000.Google Scholar
[5] Comfort, W. W., A survey of cardinal invariants. General Topology and Appl. 1(1971), no. 2, 163–199.Google Scholar
[6] Comfort, W. W., Topological groups. In: Handbook of Set-Theoretic Topology, North-Holland, Amsterdam, 1984, pp. 1143–1263.Google Scholar
[7] Dales, H. G. and Lau, A. T., The second dual of Beurling algebras. Mem. Amer. Math. Soc. 177(2005), no. 836Google Scholar
[8] Dixmier, J., C*-Algebras. North-Holland, Amsterdam, 1977.Google Scholar
[9] Edgar, G. A., Measurability in a Banach space. II. Indiana Univ. Math. J. 28(1979), no. 4, 559–579.Google Scholar
[10] Enock, M. and Schwartz, J.-M., Kac Algebras and Duality of Locally Compact Groups. Springer-Verlag, Berlin, 1992.Google Scholar
[11] Eymard, P., L’algèbra de Fourier d’un groupe localement compact. Bull. Soc. Math. France 92(1964), 181–236.Google Scholar
[12] Fremlin, D. H., Real-valued-measurable cardinals. In: Set Theory of the Reals, Israel Math. Conf. Proc. 6, Bar-Ilan Univ., Ramat Gan, 1993, pp. 151–304.Google Scholar
[13] Ghahramani, F. and McClure, J. F., The second dual algebra of the measure algebra of a compact group. Bull. London Math. Soc. 29(1997), no. 2, 223–226.Google Scholar
[14] Gardner, R. J. and Pfeffer, W. F., Borel measures. In: Handbook of Set-Theoretic Topology, North-Holland, Amsterdam, 1984, pp. 961–1043.Google Scholar
[15] Godefroy, G., Nouvelles classes d’espaces de Banach à prédual unique (d’après G. Godefroy et M. Talagrand). Seminar on Functional Analysis, 1980-1981, VI École Polytech., Palaiseau, 1981.Google Scholar
[16] Godefroy, G. and Talagrand, M., Classes d’espaces de Banach à prédual unique. C. R. Acad. Sci. Paris Sér. I Math. 292(1981), no. 5, 323–325.Google Scholar
[17] Granirer, E. E., Weakly almost periodic and uniformly continuous functionals on the Fourier algebra of any locally compact group. Trans. Amer. Math. Soc. 189(1974), 371–382.Google Scholar
[18] Granirer, E. E., Day points for quotients of the Fourier algebr A(G), extreme nonergodicity of their duals and extreme non-Arens regularity. Illinois J. Math. 40(1996), no. 3, 402–419.Google Scholar
[19] Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. II. Die Grundlehren der Mathematischen Wissenschaften 152, Springer-Verlag, New York, 1970.Google Scholar
[20] Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. I. Second edition. Grundlehren der Mathematischen Wissenschaften 115, Springer-Verlag, Berlin, 1979.Google Scholar
[21] Hu, Z., On the set of topologically invariant means on the von Neumann algebr VN(G). Illinois J. Math. 39(1995), no. 3, 463–490.Google Scholar
[22] Hu, Z., Extreme non-Arens regularity of quotients of the Fourier algebr A(G). Colloq. Math. 72(1997), no. 2, 237–249.Google Scholar
[23] Hu, Z., Inductive extreme non-Arens regularity of the Fourier algebra A(G). Studia Math. 151(2002), no. 3, 247–264.Google Scholar
[24] Jech, T., Set Theory. Springer-Verlag, Berlin, 1997.Google Scholar
[25] Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, I, II. American Mathematics Society, Providence, RI, 1997.Google Scholar
[26] Kaniuth, E. and Lau, A. T., Spectral synthesis for A(G) and subspaces of VN(G). Proc. Amer. Math. Soc. 129(2001), no. 11, 3253–3263.Google Scholar
[27] Kaniuth, E., Lau, A. T. and Schlichting, G., Weakly compactly generated Banach algebras associated to locally compact groups. J. Operator Theory 40(1998), no. 2, 323–337.Google Scholar
[28] Lacey, H. E., The Isometric Theory of Classical Banach Spaces. Die Grundlehren der athematischen Wissenschaften 208, Springer-Verlag, New York, 1974.Google Scholar
[29] Lau, A. T., Medghalchi, A. R. and Pym, J. S., On the spectrum of L∞(G). J. London Math. Soc. 48(1983), no. 1, 152–166.Google Scholar
[30] Lau, A. T. and Losert, V., On the second conjugate algebra of a locally compact group. J. London Math. Soc. 37(1988), no. 3, 464–470.Google Scholar
[31] Lau, A. T. and Losert, V., The C*-algebra generated by operators with compact support on a locally compact group. J. Funct. Anal. 112(1993), no. 1, 1–30.Google Scholar
[32] Lau, A. T. and Paterson, A. L. T., The exact cardinality of the set of topological left invariant means on an amenable locally compact group. Proc. Amer. Math. Soc. 98(1986), no. 1, 75–80.Google Scholar
[33] Neufang, M., On the Mazur property and property (X). Preprint. http://mathstat.carleton.ca/∽mneufang/mazurx.pdf Google Scholar
[34] Neufang, M., On a conjecture by Ghahramani-Lau and related problems concerning topological centres. J. Funct. Anal. 224(2005), no. 1, 217–229.Google Scholar
[35] Neufang, M., Solution to a conjecture by Hofmeier-Wittstock. J. Funct. Anal. 217(2004), no. 1, 171–180.Google Scholar
[36] Neufang, M., A unified approach to the topological centre problem for certain Banach algebras arising in abstract harmonic analysis. Arch. Math. (Basel) 82(2004), no. 2, 164–171.Google Scholar
[37] Sakai, S., C* -Algebras and W*-Algebras. Ergebnisse der Mathematik und ihrer Grenzgebiete 60, Springer-Verlag, New York, 1971.Google Scholar
[38] Solovay, R. M., Real-valued measurable cardinals. In: Axiomatic Set Theory, American Mathematical Society, Providence, RI, 1971, pp. 397–428.Google Scholar
[39] Takesaki, M., On the conjugate space of operator algebra. Tôhoku Math. J. 10(1958), 194–203.Google Scholar
[40] Takesaki, M., Theorey of Operator Alegbras. I. Operator Algebras and Non-commutative Geometry 5, Springer-Verlag, Berlin, 2002.Google Scholar