Défaut de semi-stabilité des courbes elliptiques dans le cas non ramifié

Abstract

Let 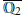$\overline{{{\mathbb{Q}}_{2}}}$ be an algebraic closure of 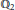${{\mathbb{Q}}_{2}}$ and 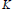$K$ be an unramified finite extension of 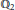${{\mathbb{Q}}_{2}}$ included in 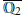$\overline{{{\mathbb{Q}}_{2}}}$. Let 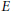$E$ be an elliptic curve defined over 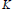$K$ with additive reduction over 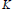$K$, and having an integral modular invariant. Let us denote by 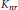${{K}_{nr}}$ the maximal unramified extension of 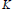$K$ contained in 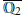$\overline{{{\mathbb{Q}}_{2}}}$. There exists a smallest finite extension $L$ of 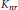${{K}_{nr}}$ over which 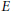$E$ has good reduction. We determine in this paper the degree of the extension 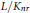$L/{{K}_{nr}}$.