Published online by Cambridge University Press: 12 October 2020
Let
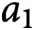 $a_1$
,
$a_1$
,
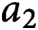 $a_2$
, and
$a_2$
, and
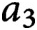 $a_3$
be distinct reduced residues modulo q satisfying the congruences
$a_3$
be distinct reduced residues modulo q satisfying the congruences
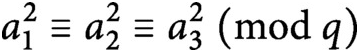 $a_1^2 \equiv a_2^2 \equiv a_3^2 \ (\mathrm{mod}\ q)$
. We conditionally derive an asymptotic formula, with an error term that has a power savings in q, for the logarithmic density of the set of real numbers x for which
$a_1^2 \equiv a_2^2 \equiv a_3^2 \ (\mathrm{mod}\ q)$
. We conditionally derive an asymptotic formula, with an error term that has a power savings in q, for the logarithmic density of the set of real numbers x for which
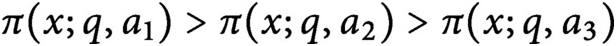 $\pi (x;q,a_1)> \pi (x;q,a_2) > \pi (x;q,a_3)$
. The relationship among the
$\pi (x;q,a_1)> \pi (x;q,a_2) > \pi (x;q,a_3)$
. The relationship among the
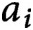 $a_i$
allows us to normalize the error terms for the
$a_i$
allows us to normalize the error terms for the
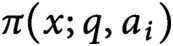 $\pi (x;q,a_i)$
in an atypical way that creates mutual independence among their distributions, and also allows for a proof technique that uses only elementary tools from probability.
$\pi (x;q,a_i)$
in an atypical way that creates mutual independence among their distributions, and also allows for a proof technique that uses only elementary tools from probability.