Article contents
Derivations Tangential to Compact Group Actions: Spectral Conditions in the Weak Closure
Published online by Cambridge University Press: 20 November 2018
Extract
Let G be a compact Lie group and a an action of G on a C*-algebra  as *-automorphisms. Let
as *-automorphisms. Let 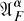 denote the set of G-finite elements for this action, i.e., the set of those
denote the set of G-finite elements for this action, i.e., the set of those 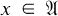 such that the orbit {αg(x):g ∊ G} spans a finite dimensional space.
such that the orbit {αg(x):g ∊ G} spans a finite dimensional space. 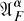 is a common core for all the *-derivations generating one-parameter subgroups of the action α. Now let δ be a *-derivation with domain
is a common core for all the *-derivations generating one-parameter subgroups of the action α. Now let δ be a *-derivation with domain 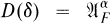 such that
such that 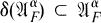 Let us pose the following two problems:
Let us pose the following two problems:
Is δ closable, and is the closure of δ the generator of a strongly continuous one-parameter group of *-automorphisms?
If
 is simple or prime, under what conditions does δ have a decomposition
is simple or prime, under what conditions does δ have a decomposition
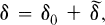
where 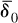 is the generator of a one-parameter subgroup of α(G) and
is the generator of a one-parameter subgroup of α(G) and 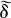 is a bounded, or approximately bounded derivation?
is a bounded, or approximately bounded derivation?
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
- 6
- Cited by


