Article contents
Diameters of Random Graphs
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For two nodes x and y of a graph G, the distance δG(x,y) is the smallest integer k such that k edges form a path from x to y; δG(x, x) = 0, and δG(x,y) = ∞ when x ≠ y and there is no path from x to y. The diameter δG is the maximum of δG (x, y) as x and y range over the nodes of G. When G is connected, δ(G) is the smallest integer k such that any two nodes of G can be joined by a path formed from at most k edges. When G is not connected, δ(G) = ∞ and there is interest in δc(G), the maximum of δ(G) over the components C of G.
For 2 ≧ n < ∞ and 0 ≧ E ≧ n(n − l)/2, let 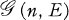 denote the set of all loopless undirected graphs with the node-set {1, …, n} and exactly E edges.
denote the set of all loopless undirected graphs with the node-set {1, …, n} and exactly E edges.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
1.
Deo, N., Breadth- and depth-first searches in graph-theoretic algorithms, Report No. TRCS-74-001 (Computer Science Centre, Indian Institute of Technology, Kanpur, 1974).Google Scholar
2.
Erdôs, P., The art of counting: Selected writings (MIT Press, Cambridge, Mass., 1973).Google Scholar
3.
Erdôs, P. and Rényi, A., On random graphs I, Publ. Math. (Debrecen)
6 (1959), 290–297.Google Scholar
5.
Moon, J. and Moser, L., Almost all (0, 1) matrices are primitive, Studia Sci. Math. Hungar.
11 (1966), 153–156.Google Scholar
- 24
- Cited by

