Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
TALL, Franklin D.
1984.
Handbook of Set-Theoretic Topology.
p.
685.
Watson, W. Stephen
1984.
Separating Points and Coloring Principles.
Canadian Mathematical Bulletin,
Vol. 27,
Issue. 4,
p.
398.
VAN DOUWEN, Eric K.
1984.
Handbook of Set-Theoretic Topology.
p.
111.
Dow, Alan
1987.
Some linked subsets of posets.
Israel Journal of Mathematics,
Vol. 59,
Issue. 3,
p.
353.
Kemoto, Nobuyuki
1989.
A note on connected submetaLindelöf spaces.
Bulletin of the Australian Mathematical Society,
Vol. 40,
Issue. 1,
p.
83.
Dow, Alan
Tall, Franklin D.
and
Weiss, William A.R.
1990.
New proofs of the consistency of the normal Moore space conjecture II.
Topology and its Applications,
Vol. 37,
Issue. 2,
p.
115.
Dow, Alan
Tall, Franklin D.
and
Weiss, William A.R.
1990.
New proofs of the consistency of the normal moore space conjecture I.
Topology and its Applications,
Vol. 37,
Issue. 1,
p.
33.
Landver, Avner
1992.
Baire numbers, uncountable Cohen sets and perfect-set forcing.
Journal of Symbolic Logic,
Vol. 57,
Issue. 3,
p.
1086.
Kemoto, Nobuyuki
1992.
Paracompactness in Perfect, Locally Lindelöf Spaces.
Rocky Mountain Journal of Mathematics,
Vol. 22,
Issue. 3,
Balogh, Zoltan T.
and
Burke, Dennis K.
1992.
A total ladder system space by ccc forcing.
Topology and its Applications,
Vol. 44,
Issue. 1-3,
p.
37.
Nyikos, Peter J.
2001.
Handbook of the History of General Topology.
Vol. 3,
Issue. ,
p.
1179.
Larson, Jean A.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
145.
Shelah, Saharon
2021.
Applying Set Theory.
Axioms,
Vol. 10,
Issue. 4,
p.
329.
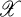 is a topological space then a sequence (Cα:α < λ) of subsets of
is a topological space then a sequence (Cα:α < λ) of subsets of 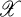 is said to be normalized if for every H ⊆ λ there exist disjoint open sets
is said to be normalized if for every H ⊆ λ there exist disjoint open sets 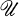 and
and 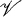 such that
such that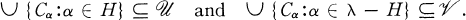
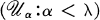 of pairwise disjoint open sets such that
of pairwise disjoint open sets such that 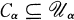 for each α < λ. As is customary, we adopt the convention that all sequences (Cα:α < λ) considered are assumed to be relatively discrete as defined in [18, p. 21]: if x ∈ Cα then there exists a neighborhood about x that intersects no Cβ for β ≠ α.
for each α < λ. As is customary, we adopt the convention that all sequences (Cα:α < λ) considered are assumed to be relatively discrete as defined in [18, p. 21]: if x ∈ Cα then there exists a neighborhood about x that intersects no Cβ for β ≠ α.