Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vergnas, Michel Las
1980.
Combinatorics 79 Part I.
Vol. 8,
Issue. ,
p.
7.
Greene, Curtis
and
Zaslavsky, Thomas
1983.
On the interpretation of Whitney numbers through arrangements of hyperplanes, zonotopes, non-Radon partitions, and orientations of graphs.
Transactions of the American Mathematical Society,
Vol. 280,
Issue. 1,
p.
97.
Pouzet, M.
1985.
Graphs and Order.
p.
592.
Tutte, W. T.
Greene, Curtis
and
Zaslavsky, Thomas
1986.
A Source Book in Matroid Theory.
p.
267.
Chia, G.L.
1997.
A bibliography on chromatic polynomials.
Discrete Mathematics,
Vol. 172,
Issue. 1-3,
p.
175.
Backman, Spencer
Hopkins, Sam
and
Traldi, Lorenzo
2018.
Fourientation activities and the Tutte polynomial.
European Journal of Combinatorics,
Vol. 67,
Issue. ,
p.
40.
Gioan, Emeric
and
Las Vergnas, Michel
2019.
The active bijection for graphs.
Advances in Applied Mathematics,
Vol. 104,
Issue. ,
p.
165.


 relative to a fixed labelling of its edges. It is shown that the number of such orientations of
relative to a fixed labelling of its edges. It is shown that the number of such orientations of  having internal activity
having internal activity  It follows that the number of orientations of
It follows that the number of orientations of  in which the resulting digraph
in which the resulting digraph  is acyclic is given by
is acyclic is given by 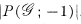 , where
, where  is the chromatic polynomial associated with
is the chromatic polynomial associated with  .
.