Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T16:18:34.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential Forms and Resolutions on Certain Analytic Spaces II. Flat Resolutions

Published online by Cambridge University Press:  20 November 2018

Vincenzo Ancona  and
Bernard Gaveau
Vincenzo Ancona
Affiliation:
Universită degli Studi Dipartmento di matematica U. DiniViale Morgagni 67/A 50134 Firenze, Italia
Bernard Gaveau
Affiliation:
Université Pierre et Marie Curie Mathématiques, tour 45–46, 5ĕme étage , place Jussieu 75252 Paris Cedex 05, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

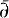This paper gives another construction of (0, p)-forms on a complex analytic space and of the operator. This construction is independent of the one in [1] and apart from the general result of Section 1 of [1], it can be read independently. As in [1], the hypotheses on 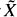S are the following: S has normal singularities, its singular locus X is smooth, the exceptional divisor in a desingularization of S is irreducible.

Keywords

32BCFS
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 4 , 01 August 1992 , pp. 728 - 749
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Ancona, V. and Gaveau, B., Differential forms and resolutions on certain analytic spaces: I Irreducible exceptional divisor, Bull. Sci. Math., to appear.Google Scholar
2. Grothendieck, A., Eléments de géométrie algébrique, EGA III. Google Scholar
3. Hartshorne, R., On the de Rham cohomology of algebraic varieties, Publ. Math. IHES.Google Scholar
4. Rossi, H.E. and Hironaka, H., On the equivalence of imbeddings of exceptional complex spaces, Math. Annalen, 156 (1964), 313–333.Google Scholar
5. Malgrange, B., Ideals of differentiable functions, Oxford University Press, 1966 Google Scholar