Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ghiloni, Riccardo
2009.
Equations and Complexity for the Dubois–Efroymson Dimension Theorem.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 2,
p.
224.

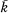 be an algebraic closure of
be an algebraic closure of 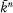 (n some integer greater than 0) which is the set of zeros of some polynomials in
(n some integer greater than 0) which is the set of zeros of some polynomials in 