Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lorentz, G. G.
and
Macphail, M. S.
1953.
Direct theorems on methods of summability III: absolute summability functions.
Mathematische Zeitschrift,
Vol. 59,
Issue. 1,
p.
231.
Chillingworth, H.R.
1957.
On Matrix Transformations of Certain Sequence Spaces.
Indagationes Mathematicae (Proceedings),
Vol. 60,
Issue. ,
p.
578.
Tietz, Hubert
1971.
Negative Resultate �ber Tauber-Bedingungen.
Monatshefte f�r Mathematik,
Vol. 75,
Issue. 1,
p.
69.
Petersen, G.M
1975.
Tauberian conditions for a class of matrices.
Journal of Approximation Theory,
Vol. 13,
Issue. 2,
p.
146.
Devos, Robert
1978.
Category of sequences of zeros and ones in some FK spaces.
Glasgow Mathematical Journal,
Vol. 19,
Issue. 2,
p.
121.
Parameswaran, Mangalam R.
1978.
On a generalization of a theorem of Meyer-K�nig.
Mathematische Zeitschrift,
Vol. 162,
Issue. 3,
p.
201.
Nagainik, A. F.
1981.
Absolute summation of sequences by binary methods.
Ukrainian Mathematical Journal,
Vol. 33,
Issue. 2,
p.
157.
Kuttner, B.
1982.
Absolute summability functions for Hausdorff methods.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 1,
p.
51.
Butković, D.
Kraljević, H.
and
Sarapa, N.
1987.
Functional Analysis II.
Vol. 1242,
Issue. ,
p.
396.
Lorentz, G. G.
1997.
Mathematics from Leningrad to Austin.
p.
195.
Lorentz, G. G.
1997.
Mathematics from Leningrad to Austin.
p.
206.
Lorentz, G. G.
1997.
Mathematics from Leningrad to Austin.
p.
206.
Lorentz, G. G.
1997.
Mathematics from Leningrad to Austin.
p.
195.
Lorentz, G. G.
1997.
Mathematics from Leningrad to Austin.
p.
164.
Fridy, John A
and
Khan, Mohammad K
1998.
Tauberian Theorems via Statistical Convergence.
Journal of Mathematical Analysis and Applications,
Vol. 228,
Issue. 1,
p.
73.
Fridy, J.A.
and
Khan, M.K.
2003.
Statistical gap Tauberian theorems in metric spaces.
Journal of Mathematical Analysis and Applications,
Vol. 282,
Issue. 2,
p.
744.


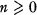 , the number of n satisfying the inequality
, the number of n satisfying the inequality 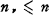 . Suppose that A is a linear method of summation corresponding to the transformation
. Suppose that A is a linear method of summation corresponding to the transformation