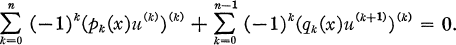Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-15T06:23:04.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Disconjugacy Criteria for Nonselfadjoint Differential Equations of Even Order

Published online by Cambridge University Press:  20 November 2018

Kurt Kreith
Kurt Kreith*
Affiliation:
University of California, Davis, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Disconjugacy criteria have been established for linear selfadjoint differential equations of order 2n by Sternberg [4] and Ahlbrandt [1]. Such differential equations can be written in the form

1.1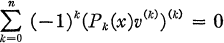

where it is assumed that the coefficients are real and that Pn(x) ≠ 0. We shall be interested in nontrivial solutions v(x) of (1.1), which satisfy

1.2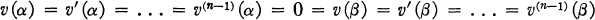

for distinct points α and β. The smallest β> α such that (1.2) is satisfied nontrivially by a solution of (1.1), is denoted by μ1(α) and called the first conjugate point of x = α with respect to (1.1). If no such conjugate point exists we write μ1(α) = ∞, and say that (1.1) is disconjugate on [α, ∞).

The principal purpose of this paper is to generalize these disconjugacy criteria to the general linear nonselfadjoint differential equation of the form

1.3

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 4 , August 1971 , pp. 644 - 652
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Ahlbrandt, C. D., Disconjugacy criteria for self adjoint differential systems, J. Differential Equations 6 (1969), 271–295.Google Scholar
2. Barrett, J., Fourth order boundary value problems and comparison theorems, Can. J. Math. 13 (1961), 625–638.Google Scholar
3. Howard, H. C., Some oscillation criteria for general self adjoint differential equations, J. London Math. Soc. 43 (1968), 401–406.Google Scholar
4. Kaufman, H. and Sternberg, R., A two-point boundary problem for ordinary self adjoint differential equations of even order, Duke Math. J. 20 (1953), 527–531.Google Scholar
5. Kreith, K., A comparison theorem for conjugate points of general self adjoint differential equations, Proc. Amer. Math. Soc. 25 (1970), 656–661.Google Scholar
6. Reid, W. T., Riccati matrix differential equations and nonoscillation criteria for associated linear differential systems, Pacific J. Math. 13 (1963), 665–685.Google Scholar
7. Sternberg, R. L., Variational methods and nonoscillation theorems for systems of differential equations, Duke Math. J. 19 (1956), 311–322.Google Scholar