Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T13:13:19.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Distance From Projections to Nilpotents

Published online by Cambridge University Press:  20 November 2018

Gordon W. Macdonald
Gordon W. Macdonald*
Affiliation:
Department of Mathematics and Computer Science, University of Prince Edward Island, Charlottetown, Prince Edward Island, CIA 4P3
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The distance from an arbitrary rank-one projection to the set of nilpotent operators, in the space of k × k matrices with the usual operator norm, is shown to be sec(π/(k:+2))/2. This gives improved bounds for the distance between the set of all non-zero projections and the set of nilpotents in the space of k × k matrices. Another result of note is that the shortest distance between the set of non-zero projections and the set of nilpotents in the space of k × k matrices is .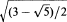

Keywords

47A5815A99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 4 , 01 August 1995 , pp. 841 - 851
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Hedlund, J.H., Limits of nilpotent and quasinilpotent operators, Michigan Math. J. 19(1972), 249–255.Google Scholar
2. Herrero, D., Toward a spectral characterization of the set of norm limits of nilpotent operators, Indiana Univ. Math. J. 24(1975), 847–864.Google Scholar
3. Herrero, D., Quasidiagonality, similarity and approximation by nilpotent operators, Indiana Univ. Math. J. 30(1981), 199–233.Google Scholar
4. Herrero, D., Unitary orbits of power partial isometries and approximation by block-diagonal nilpotents, Topics in Modern Operator Theory, Timisoara-Herculane, (Romania), June 2-11, 1980. Oper. Theory Adv. Appl. 2(1981), 171–210.Google Scholar
5. Herrero, D., Approximation ofHilbert Space Operators Volume I, Pitman Res. Notes Math. 72, London, 1982.Google Scholar
6. Power, S., The distance to upper triangular operators, Math. Proc. Cambridge Philos. Soc. 88(1980), 327–329.Google Scholar
7. Salinas, N., On the distance to the set of compact perturbations of nilpotent operators, J. Operator Theory 3(1980), 179–194.Google Scholar