Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T09:56:50.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Distance Functions and Orlicz-Sobolev Spaces

Published online by Cambridge University Press:  20 November 2018

D. E. Edmunds  and
R. M. Edmunds
D. E. Edmunds
Affiliation:
University of Sussex, Brighton, U.K
R. M. Edmunds
Affiliation:
University College, Cardiff, U.K
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ∧ be a bounded, non-empty, open subset of Rn and given any x in Rn, let

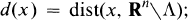
let k ∊ N and suppose that p ∞ (1, ∞). It is known (c.f. e.g. [4]) that if u belongs to the Sobolev space WKp(∧) and u/dk ∊ Lp(∧), then 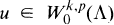. Further results in this direction are given in [5] and [9]. Moreover, if m is the mean distance function in the sense of [2], then it turns out that

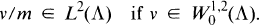
Under appropriate smoothness conditions on the boundary of ∧, m and d are equivalent, and thus 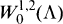may in this case be characterized as the subspace of W1,2(∧) consisting of all functions u ∊ W1,2(∧) such that u/d ∊ L2(∧). Further results in this direction are given in [5] and [9]. Moreover, if m is the mean distance function in the sense of [2], then it turns out that

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 5 , 01 October 1986 , pp. 1181 - 1198
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Adams, R. A., Sobolev spaces (Academic Press, New York, 1975).Google Scholar
2. Davies, E. B., Some norm bounds and quadratic form inequalities for Schrödinger operators II, J. Operator Theory 12 (1984), 177–196.Google Scholar
3. Donaldson, T. and Trudinger, N., Orlicz-Sobolev spaces and embedding theorems, J. Functional Anal. 8 (1971), 52–75.Google Scholar
4. Edmunds, D. E. and Evans, W. D., Spectral theory and differential operators (forthcoming book).CrossRefGoogle Scholar
5. Edmunds, D. E., Kufner, A. and Rakosnik, J., Embeddings of Sobolev spaces with weights of power type, Z. Analysis Anwendungen 4 (1985), 25–34.Google Scholar
6. Friedman, A., Partial differential equations (Holt, Rinehart, Winston, New York, 1968).Google Scholar
7. Stein, E. M., Singular integrals and differentiability properties of functions (Princeton University Press, Princeton, 1970).Google Scholar
8. Triebel, H., Interpolation theory, function spaces, differential operators (VEB Deutscher Verl. Wissenschaften, Berlin, 1978, and North-Holland Publishing Co., Amsterdam, New York, Oxford, 1978).Google Scholar
9. Triebel, H., Remark on a paper by D. E. Edmunds, A. Kufner and J. Rakosnik, “Embeddings on Sobolev spaces with weights of power type”, Z. Analysis Anwendungen 4 (1985), 35–38.Google Scholar