No CrossRef data available.
Article contents
A Distortion Theorem for Analytic Maps of Annuli
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Every abstract open Riemann surface can be made "concrete" (in the terminology of (1)) by considering it as a covering surface (in general branched) of the complex plane 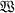 by means of a suitable projection map p. Since this covering map is not unique, it seems natural to single out some such maps by an extremal property. The use of Riemannian metrics compatible with the conformai structure on the given surface
by means of a suitable projection map p. Since this covering map is not unique, it seems natural to single out some such maps by an extremal property. The use of Riemannian metrics compatible with the conformai structure on the given surface 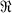 for the study of $1 is well known ; from the point of view of differential geometry it suggests an investigation of the distortion caused by p between such a metric ds^ and the Euclidean metric of
for the study of $1 is well known ; from the point of view of differential geometry it suggests an investigation of the distortion caused by p between such a metric ds^ and the Euclidean metric of 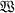 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1965
References
1.
Behnke, H. and Sommer, F., Théorie der analytischen Funktionen einer komplexen Verdnderlichen (Berlin, 1955).Google Scholar
3.
Castonguay, C. E. and Helfenstein, H. G., On analytic maps of the pseudosphere, Monatsh. Math., 68 (1964), 97–101.Google Scholar
5.
Helfenstein, H. G., Conformai maps with least distortion, Can. J. Math., 7 (1955), 306–313.Google Scholar

