Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T10:32:20.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Distributions invariantes sur les groupes réductifs quasi-déployés

Published online by Cambridge University Press:  20 November 2018

François Courtès
François Courtès*
Affiliation:
Université de Poitiers, SP2MI - Département de Mathématiques, Téléport 2 - Boulevard Marie et Pierre Curier, 86962 Futuroscope Chasseneuil Cedex, France e-mail: courtes@mathlabo.univ-poitiers.fr
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soit $F$ un corps local non archimédien, et 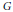$G$ le groupe des $F$-points d’un groupe réductif connexe quasi-déployé défini sur $F$. Dans cet article, on s’intéresse aux distributions sur 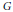$G$ invariantes par conjugaison, et à l’espace de leurs restrictions à l’algèbre de Hecke 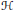$\mathcal{H}$ des fonctions sur 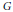$G$ à support compact biinvariantes par un sous-groupe d’Iwahori 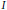$I$ donné. On montre tout d’abord que les valeurs d’une telle distribution sur 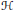$\mathcal{H}$ sont entièrement déterminées par sa restriction au sous-espace de dimension finie des éléments de 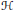$\mathcal{H}$ à support dans la réunion des sous-groupes parahoriques de 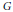$G$ contenant 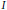$I$. On utilise ensuite cette propriété pour montrer, moyennant certaines conditions sur 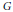$G$, que cet espace est engendré d’une part par certaines intégrales orbitales semi-simples, d’autre part par les intégrales orbitales unipotentes, en montrant tout d’abord des résultats analogues sur les groupes finis.

Keywords

22E3520G4Reductive p-adic groupsorbital integralsinvariant distributions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 5 , 01 October 2006 , pp. 897 - 999
Copyright
Copyright © Canadian Mathematical Society 2006

References

Références

[1] Bala, P. et Carter, R. W., Classes of unipotent elements in simple algebraic groups. I. Math. Proc. Cambridge Philos. Soc. 79(1976), no. 3, 401–425.Google Scholar
[2] Borel, A. et al. Conjugacy classes. Lecture Notes in Mathematics 131, Springer-Verlag,.Google Scholar
[3] Bourbaki, N.. Groupes et algèbres de Lie, chapitre 6: Systèmes de racines. Hermann, Paris,.Google Scholar
[4] Bruhat, F. et Tits, J., Groupes réductifs sur un corps local. Inst. Hautes Études Sci. Publ. Math. 41(1972), 5–251. Inst. Hautes Études Sci Publ. Math. 60(1984), 5–184.Google Scholar
[5] Carter, R. W., Finite groups of Lie type. John Wiley, New York, 1985.Google Scholar
[6] Cartier, P., Représentation of p-adic groups: a survey. Dans: Automorphic Forms, Representations and L-functions. Proc. Sympos. Pure Math. 33, American Mathematical Society, Providence, RI, pp. 111–155.Google Scholar
[7] Casselman, W., Introduction to the theory of admissible representation of p-adic reductive groups, 1977, notes non publiées.Google Scholar
[8] Chevalley, C., Sur certains groupes simples. Tôhoku Math. J. (1955), 14–66.Google Scholar
[9] Clozel, L., Orbitals integrals on p-adic groups: a proof of the Howe conjecture. Ann. of Math. 129(1989), no. 2, 237–251.Google Scholar
[10] Clozel, L., The fundamental lemma for stable base change. Duke Math. J. 61(1990), pp. 255–302.Google Scholar
[11] Curtis, C.W. et Reiner, I., Methods of representation theory. Vol. 1. With applications to finite groups and orders., Wiley Interscience, NY, 1981.Google Scholar
[12] DeBacker, S., Parametrizing nilpotent orbits via Bruhat-Tits theory. Ann. of Math. 156(2002), 295–332.Google Scholar
[13] DeBacker, S., Parametrizing conjugacy classes of maximal unramified tori via Bruhat-Tits theory. Preprint disponible à: http://www.math.lsa.umich.edu/∼smdbackr Google Scholar
[14] Digne, F. et Michel, J., Groupes réductifs non connexes. Ann. Sci. École Norm. Ssup. 27(1994), no. 3, 345–406.Google Scholar
[15] Kazhdan, D., Cuspidal geometry of p-adic groups. J. Analyse Math. 47(1986), 1–36.Google Scholar
[16] Kazhdan, D., Representation of groups over close local fields. J. Analyse Math. 47(1986), 175–179.Google Scholar
[17] Lang, S., Algebraic groups over finite fields. Amer. J. Math. 78(1956), 555–563.Google Scholar
[18] Lusztig, G., Unipotent characters of the even orthogonal groups over a finite field. Trans. Amer. Math. Soc. 272(1982), 733–751.Google Scholar
[19] Lusztig, G., On the unipotent characters of the exceptional groups over finite fields. Invent.Math. 60(1980), 173–192.Google Scholar
[20] Lusztig, G., Characters of Reductive Groups Over a Finite Field. Annals of Mathematics Studies 107, Princeton University Press, Princeton, NJ, 1984.Google Scholar
[21] Moy, A. et Prasad, G., Unramified minimal K-types for p-adic groups. Invent.s Math. 116(1994), no. 1-3, 393–408.Google Scholar
[22] Pommerening, K., Über die unipotenten Klassen reduktiver Gruppen. J. Algebra 49(1977), 525–536 65(1980), 373–398.Google Scholar
[23] Schneider, P. et Stuhler, U., Representation theory and sheaves on the Bruhat-Tits building. Inst. Hautes Études Sci. Publ. Math. 85(1997), 97–191.Google Scholar
[24] Serre, J. P., Cohomologie galoisienne. Quatrième édition. Lecture Notes in Mathematics 5, Springer-Verlag, Berlin, 1973.Google Scholar
[25] Tits, J., Reductive groups over local fields. Dans: Automorphic Forms, Representations and L-functions. Proc. Sympos. Pure Math. 33, American Mathematical Society, Providence, RI, pp. 29–69.Google Scholar
[26] Waldspurger, J. L., Quelques questions sur les intégrales orbitales unipotentes et les algèbres de Hecke. Bull. Soc. Math. France 124(1996), no. 1, 1–34.Google Scholar