Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T03:46:39.487Z Has data issue: false hasContentIssue false
  • English
  • Français

The Dunford-Pettis Property for Symmetric Spaces

Published online by Cambridge University Press:  20 November 2018

Anna Kamińska  and
Mieczysław Mastyło
Anna Kamińska
Affiliation:
Department of Mathematical Sciences, The University of Memphis, Memphis, TN 38152, USA email: kaminska@msci.memphis.edu
Mieczysław Mastyło
Affiliation:
Faculty of Mathematics and Computer Science, A. Mickiewicz University, Matejki 48/49, 60-769 Poznań, Poland email: mastylo@math.amu.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A complete description of symmetric spaces on a separable measure space with the Dunford-Pettis property is given. It is shown that 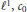${{\ell }^{1}},{{c}_{0}}$ and 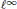${{\ell }^{\infty }}$ are the only symmetric sequence spaces with the Dunford- Pettis property, and that in the class of symmetric spaces on 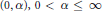$(0,\,\alpha ),\,0\,<\,\alpha \,\le \,\infty$, the only spaces with the Dunford-Pettis property are 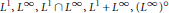${{\text{L}}^{1}},{{\text{L}}^{\infty }},{{\text{L}}^{1}}\cap {{\text{L}}^{\infty }},{{\text{L}}^{1}}+{{\text{L}}^{\infty }},{{({{\text{L}}^{\infty }})}^{\text{o}}}$ and 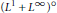${{({{\text{L}}^{1}}+{{\text{L}}^{\infty }})}^{\text{o}}}$, where 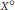${{\text{X}}^{\text{o}}}$ denotes the norm closure of 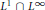${{\text{L}}^{1}}\cap {{\text{L}}^{\infty }}$ in 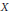$X$. It is also proved that all Banach dual spaces of 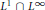${{\text{L}}^{1}}\cap {{\text{L}}^{\infty }}$ and 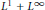${{\text{L}}^{1}}+{{\text{L}}^{\infty }}$ have the Dunford-Pettis property. New examples of Banach spaces showing that the Dunford-Pettis property is not a three-space property are also presented. As applications we obtain that the spaces 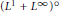${{({{\text{L}}^{1}}+{{\text{L}}^{\infty }})}^{\text{o}}}$ and 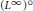${{({{\text{L}}^{\infty }})}^{\text{o}}}$ have a unique symmetric structure, and we get a characterization of the Dunford-Pettis property of some Köthe-Bochner spaces.

Keywords

46E3046B42
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 4 , 01 August 2000 , pp. 789 - 803
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Abramovich, Y. A. and Wojtaszczyk, P., On the uniqueness of order in the spaces p and Lp(0, 1). Mat. Zametki 18(1975), 313–325.Google Scholar
[2] Aliprantis, C. D. and Burkinshaw, O., Positive Operators. Academic Press, New York, London, 1985.Google Scholar
[3] Bennett, C. and Sharpely, R., Interpolation of Operators. Academic Press, Orlando 1988.Google Scholar
[4] Bergh, J. and Löfström, J., Interpolation Spaces, An Introduction. Grundhlehren Math. Wiss. 223, Springer-Verlag, Berlin-Heidelberg-New York, 1976.Google Scholar
[5] Bourgain, J., New Banach space properties of the disc algebra and H. Acta Math. 152(1984), 1–48.Google Scholar
[6] Bourgain, J., The Dunford-Pettis property for the ball algebras, the polydisc-algebras and the Sobolev spaces. Studia Math. 77(1984), 245–253.Google Scholar
[7] Calderón, A. P., Spaces between L1 and L∞ and the theorems of Marcinkiewicz. Studia Math. 26(1996), 273–299.Google Scholar
[8] Castillo, J. M. F. and Gonzalez, M., The Dunford-Pettis property is not a three-space property. Israel J. Math. 81(1993), 297–299.Google Scholar
[9] Castillo, J. M. F. and Gonzalez, M., Three-space problems in Banach space theory. Lecture Notes in Math. 1667, Springer-Verlag, Berlin, 1997.Google Scholar
[10] Cilia, R., A remark on the Dunford-Pettis property in L1(μ, X). Proc. Amer. Math. Soc. 120(1994), 183–184.Google Scholar
[11] Cembranos, P., The hereditary Dunford-Pettis property in C(K, E). Illinois J. Math. 31(1987), 365–373.Google Scholar
[12] Chaumat, J., Une généralisation d’un théorème de Dunford-Pettis. Université de Paris XI, Orsay, 1974.Google Scholar
[13] Contreras, M. D. and Diaz, S., On the Dunford-Pettis property in spaces of vector-valued bounded functions. Bull. Austral.Math. Soc. 53(1990), 131–134.Google Scholar
[14] Diestel, J., A survey of results related to the Dunford-Pettis property. Integration, topology and geometry in linear spaces, Proc. Conf. Chapel Hill, NC, 1979, Contemp.Math. 2(1980), 15–60.Google Scholar
[15] Fremlin, D. H., Stable subspaces of L1 + L∞. Proc. Cambridge Philos. Soc. 64(1968), 625–643.Google Scholar
[16] Grothendieck, A., Sur les applications linéaires faiblement compactes d’espaces du type C(K). Canad. J. Math. 5(1953), 129–173.Google Scholar
[17] Hernandez, F. L. and Kalton, N. J., personal communication.Google Scholar
[18] Johnson, W. B., Maurey, B., Schechtmann, G. and Tzafriri, L., Symmetric Structures in Banach Spaces. Mem. Amer.Math. Soc. 217, 1979.Google Scholar
[19] de Jonge, E., The semi-M-property for normed Riesz spaces. Compositio Math. 34(1977), 147–172.Google Scholar
[20] Kalton, N. J., Lattice Structures on Banach Spaces. Mem. Amer. Math. Soc. 493, 1993.Google Scholar
[21] Kantorovich, L. V. and Akilov, G. P., Functional Analysis. 2nd rev. ed., “Nauka”, Moscow, 1977; English transl., Pergamon Press, 1982.Google Scholar
[22] Kislyakov, S. V., The Dunford-Pettis, Pełczyński and Grothendieck conditions. (Russian) Dokl. Akad. Nauk SSSR 225(1975), 1252–1255.Google Scholar
[23] Krein, S. G., Petunin, Y. U. and Semenov, E. M., Interpolation of Linear Operators. (Russian) Moscow, 1978; English transl., Amer.Math Soc., Providence, 1982.Google Scholar
[24] Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. Springer-Verlag, Berlin-New York, Vol. I, 1977. Vol. II, 1979.Google Scholar
[25] Lozanovskii, G. Ya., Transformations of ideal Banach spaces by means of concave functions. (Russian) Qualitative and Approximate methods for the investigation of Operator Equations 3(1978), Yaroslav. Gos. Univ., Yaroslavl, 122–148.Google Scholar
[26] W. Luxemburg, A. J. and Zaanen, A. C., Riesz Spaces II. North-Holland, Amsterdam, 1983.Google Scholar
[27] Novikov, S. Ya., Boundary spaces for inclusion map between RIS. Collect. Math. 44(1993), 211–215.Google Scholar
[28] Pełczyński, A., Banach spaces of analytic functions and absolutely summable operators. CBMS, Regional Conference Series in Mathematics 30, Amer. Math. Soc, Providence, RI, 1977.Google Scholar
[29] Wnuk, W., spaces with the Dunford-Pettis property. Comment.Math. PraceMat. (2) 30(1991), 483–489.Google Scholar
[30] Wnuk, W., Banach lattices with the weak Dunford-Pettis property. Atti. Sem. Mat. Fis. Univ.Modena 42(1994), 227–236.Google Scholar
[31] Wojtaszczyk, P., Banach Spaces for Analysts. Cambridge University Press, 1996.Google Scholar