Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-10T14:20:20.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Eigenpolytopes of Distance Regular Graphs

Published online by Cambridge University Press:  20 November 2018

C. D. Godsil
C. D. Godsil*
Affiliation:
Combinatorics and Optimization, University of Waterloo Waterloo, Ontario, N2L 3G1
*
e-mail: cgodsil@math.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

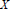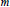Let $X$ be a graph with vertex set $V$ and let $A$ be its adjacency matrix. If $E$ is the matrix representing orthogonal projection onto an eigenspace of $A$ with dimension $m$, then $E$ is positive semi-definite. Hence it is the Gram matrix of a set of 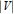$\left| V \right|$ vectors in 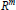${{R}^{m}}$. We call the convex hull of a such a set of vectors an eigenpolytope of 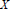$X$. The connection between the properties of this polytope and the graph is strongest when 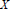$X$ is distance regular and, in this case, it is most natural to consider the eigenpolytope associated to the second largest eigenvalue of $A$. The main result of this paper is the characterisation of those distance regular graphs 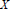$X$ for which the 1-skeleton of this eigenpolytope is isomorphic to 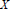$X$.

Keywords

05E3005C50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 739 - 755
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

Support from a National Sciences and Engineering Council of Canada operating grant is gratefully acknowledged

References

1. Balinski, M., On the graph structure of convex polyhedra in n-space. Pacific J. Math. 11(1961), 431–434.Google Scholar
2. Brøndsted, A., An Introduction to Convex Polytopes. Springer, New York, 1983.Google Scholar
3. Brouwer, A. E., Cohen, A. M. and Neumaier, A., Distance-Regular Graphs. Springer, Berlin, 1989.Google Scholar
4. Delsarte, P., An algebraic approach to the association schemes of coding theory. Philips Research Reports Supplements 10, 1973.Google Scholar
5. Godsil, C. D., Graphs, groups and polytopes. In: Combinatorial Mathematics. (eds. by Holton, D. A. and Jennifer Seberry), Lecture Notes in Math. 686, Springer, Berlin, 1978. 157–164.Google Scholar
6. Godsil, C. D., Bounding the diameter of distance regular graphs. Combinatorica 8(1988), 333–343.Google Scholar
7. Godsil, C. D., Algebraic Combinatorics. Chapman and Hall, New York, 1993.Google Scholar
8. Godsil, C. D., Equitable partitions. In: Combinatorics, Paul Erdȍs is Eighty, Vol. I. (eds. D. Miklós, V. T. S´os, T. Szȍnyi), Jànos Bolyai Mathematical Society, Budapest, 1993. 173–192.Google Scholar
9. Godsil, C. D. and Martin, W. J., Quotients of association schemes. J. Combin. Theory Ser. A 69(1995), 185–199.Google Scholar
10. Lambeck, E. W., Contributions to the Theory of Distance Regular Graphs. Ph. Thesis, D., Technical University Eindhoven, 1990.Google Scholar
11. Licata, C. and Powers, D. L., A surprising property of some regular polytopes. Scientia 1(1988), 73–80.Google Scholar
12. Meyerowitz, A., Cycle-balanced partitions in distance-regular graphs. submitted.Google Scholar
13. Neumaier, A., Characterization of a class of distance-regular graphs. J. Reine Angew. Math. 357(1985), 182–192.Google Scholar
14. Powers, D. L., The Petersen polytopes. Technical Report, Clarkson University, 1986.Google Scholar
15. Powers, D. L., Eigenvectors of distance-regular graphs. SIAM J. Matrix Anal. Appl. 9(1988), 399–407.Google Scholar
16. Terwilliger, P., A new feasibility condition for distance-regular graphs. Discrete Math. 61(1986), 311–315.Google Scholar
17. Terwilliger, P., Root systems and the Johnson and Hamming graphs. European J. Combin. 8(1987), 73–102.Google Scholar
18. Zhu, R., Distance-regular graphs with an eigenvalue of multiplicity four. J.Combin. Theory Ser.B 57(1993), 157–182.Google Scholar