Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:16:46.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary Proof of the Fundamental Lemma For a Unitary Group

Published online by Cambridge University Press:  20 November 2018

Yuval Z. Flicker
Yuval Z. Flicker*
Affiliation:
Department of Mathematics the Ohio State University231 W. 18th Avenue Columbus, OH 43210-1174 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The fundamental lemma in the theory of automorphic forms is proven for the (quasi-split) unitary group 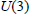$U(3)$ in three variables associated with a quadratic extension of 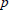$p$-adic fields, and its endoscopic group 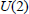$U(2)$, by means of a new, elementary technique. This lemma is a prerequisite for an application of the trace formula to classify the automorphic and admissible representations of 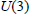$U(3)$ in terms of those of 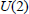$U(2)$ and base change to 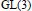$\text{GL(3)}$. It compares the (unstable) orbital integral of the characteristic function of the standard maximal compact subgroup 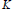$K$ of 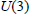$U(3)$ at a regular element (whose centralizer 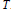$T$ is a torus), with an analogous (stable) orbital integral on the endoscopic group 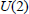$U(2)$. The technique is based on computing the sum over the double coset space 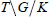$T\backslash G/K$ which describes the integral, by means of an intermediate double coset space 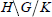$H\backslash G/K$ for a subgroup 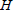$H$ of 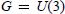$G=U(3)$ containing 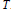$T$. Such an argument originates from Weissauer's work on the symplectic group. The lemma is proven for both ramified and unramified regular elements, for which endoscopy occurs (the stable conjugacy class is not a single orbit).

Keywords

22E3511F7011F8511S37
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 1 , 01 February 1998 , pp. 74 - 98
Copyright
Copyright © Canadian Mathematical Society 1998

References

[A] Arthur, J., On some problems suggested by the trace formula. Lecture Notes in Math. 1041 (1984), 1–49.Google Scholar
[F1] Flicker, Y., On the symmetric square. Unit elements. Pacific J. Math. 175 (1996), 507–526.Google Scholar
[F2] Flicker, Y., Unitary quasi-lifting: applications. Trans. Amer. Math. Soc. 294 (1986), 553–565.Google Scholar
[F3] Flicker, Y., Packets and liftings for U (3). J. Anal. Math. 50 (1988), 19–63.Google Scholar
[F4] Flicker, Y., Base change trace identity for U (3). J. Anal. Math. 52 (1989), 39–52.Google Scholar
[F5] Flicker, Y., Matching of orbital integrals on GL(4) and GSp(2). To appear: Mem. Amer. Math. Soc.Google Scholar
[FH] Flicker, Y., Hakim, J., Quaternionic distinguished representations. Amer. J. Math. 116 (1994), 683–736.Google Scholar
[GP] Gelbart, S. and Piatetski-Shapiro, I., Automorphic forms and L-functions for the unitary group. Lecture Notes in Math. 1041 (1984), 141–184.Google Scholar
[K] Kazhdan, D., On lifting. Lecture Notes in Math. 1041 (1984), 209–249.Google Scholar
[L] Langlands, R., Les débuts d’une formule des traces stables. Publ. Math. Univ. Paris VII 13 (1980).Google Scholar
[LR] Langlands, R. and Ramakrishnan, D. (eds.), The zeta functions of Picard modular surfaces.Les Publications CRM, Montreal, 1992.Google Scholar
[LS] Langlands, R. and Shelstad, D., On the definition of transfer factors. Math. Ann. 278 (1987), 219–271.Google Scholar
[Wa] Waldspurger, J.-L., Le lemme fondamental implique le transfert. Publ. Math. IHES (1996).Google Scholar
[W] Weissauer, R., A special case of the fundamental lemma I, II, III. Preprints.Google Scholar
[Z] Zinoviev, D., A relation of orbital integrals on SO(5) and PGL(2). To appear: Israel J. Math. (1998).Google Scholar