Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T05:39:49.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary Symmetric Polynomials in Numbers of Modulus 1

Published online by Cambridge University Press:  20 November 2018

Donald I. Cartwright  and
Tim Steger
Donald I. Cartwright
Affiliation:
School of Mathematics and Statistics University of Sydney N.S.W. 2006 Australia
Tim Steger
Affiliation:
Istituto di Matematica e Fisica Università di Sassari via Vienna 2 07100 Sassari Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe the set of numbers 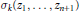${{\sigma }_{k}}\left( {{z}_{1}},\cdot \cdot \cdot ,{{z}_{n+1}} \right)$, where 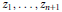${{z}_{1}},\cdot \cdot \cdot ,{{z}_{n+1}}$ are complex numbers of modulus 1 for which 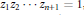${{z}_{1}}{{z}_{2}}\cdot \cdot \cdot {{z}_{n+1}}=1$, and 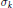${{\sigma }_{k}}$ denotes the $k$-th elementary symmetric polynomial. Consequently, we give sharp constraints on the coefficients of a complex polynomial all of whose roots are of the same modulus. Another application is the calculation of the spectrum of certain adjacency operators arising naturally on a building of type 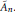${{\overset{\sim }{\mathop{\text{A}}}\,}_{n}}$.

Keywords

05E0533C4530C1551E24
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 2 , 01 April 2002 , pp. 239 - 262
Copyright
Copyright © Canadian Mathematical Society 2002

References

[Ca1] Cartwright, D. I., Harmonic functions on buildings of type Ãn. In: Random Walks and Discrete Potential Theory, (eds., M. Picardello and W. Woess), Symposia Math. XXXIX, Cambridge Univ. Press, 1999, 104–138.Google Scholar
[Ca2] Cartwright, D. I., Spherical harmonic analysis on buildings of type Ãn. Monatsh. Math., to appear.Google Scholar
[CM] Cartwright, D. I. and Młotkowski, W., Harmonic analysis for groups acting on triangle buildings. J. Austral. Math. 56 (1994), 345–383.Google Scholar
[Ll] Lloyd, N. G., Degree Theory. Cambridge Tracts in Math. 73, Cambridge Univ. Press, 1978.Google Scholar
[Mac1] Macdonald, I. G., Spherical functions on a group of p-adic type. Ramanujan Inst. Publications 2 , University of Madras, 1971.Google Scholar
[Mac2] Macdonald, I. G., Symmetric functions and Hall polynomials, second edition. Oxford Univ. Press, 1995.Google Scholar
[MZ] Mantero, A. M. and Zappa, A., Spherical functions and spectrum of the Laplace operators on buildings of rank 2. Boll. Un. Mat. Ital. B (6) 8 (1994), 419–475.Google Scholar
[Ro] Ronan, M., Lectures on buildings. Academic Press, 1989.Google Scholar
[Sz] Szegö, G., Orthogonal Polynomials. Amer. Math. Soc. Colloq. Publ. XXIII, Amer. Math. Soc., Providence, Rhode Island, 1939.Google Scholar