Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T17:23:54.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Endomorphism Rings of Quasi-Injective Modules

Published online by Cambridge University Press:  20 November 2018

B. L. Osofsky
B. L. Osofsky*
Affiliation:
Rutgers, The State University, New Brunswick, N.J.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

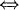Y. Utumi (14 and 15) obtained some interesting results on self-injective rings. He showed that, if R is right self-injective, then so is R/J, where J is the Jacobson radical of R. Also, if R is right self-injective and regular, then R is left self-injective for any set of orthogonal idempotents 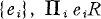is an essential extension of . This note extends these results to endomorphism rings of quasi-injective modules.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 895 - 903
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

This research was partially supported by the National Science Foundation under grant GP-4226.

References

1. Cartan, H. and Eilenberg, S., Homologuai algebra (Princeton Univ. Press, Princeton, N.J., 1956).Google Scholar
2. Eckmann, B. and Schopf, A., Ûber injektive Moduln, Arch. Math. 4 (1956), 75–78.Google Scholar
3. Faith, C., Lectures on injective modules and quotient rings (Springer-Verlag, New York, 1967).10.1007/BFb0074319CrossRefGoogle Scholar
4. Johnson, R. E., The extended centraliser of a ring over a module, Proc. Amer. Math. Soc. 2 1951), 891–895.Google Scholar
5. Johnson, R. E., Quotient rings of rings with zero singular ideal, Pacific J. Math. 11 (1961), 1385–1392.Google Scholar
6. Johnson, R. E. and Wong, E. T., Self-injective rings, Can. Math. Bull. 2 (1959), 167–173.Google Scholar
7. Johnson, R. E. and Wong, E. T., Quasi-injective modules and irreducible rings, J. London Math. Soc. 36 (1961), 260–268.Google Scholar
8. Lambek, J., On Utumïs ring of quotients, Can. J. Math. 15 (1963), 363–370.Google Scholar
9. Miyashita, Y., On quasi-injective modules, J. Fac. Sci. Hokkaido Univ. Ser. I 18 (1965), 158–187.Google Scholar
10. von Neumann, J., Continuous geometry (Princeton Univ. Press, Princeton, N.J., 1960).Google Scholar
11. Utumi, Y., On a theorem on modular lattices, Proc. Japan Acad. 35 (1959), 16–21.Google Scholar
12. Utumi, Y., On continuous regular rings, Can. Math. Bull. 4 (1961), 63–69.Google Scholar
13. Utumi, Y., On rings of which any one-sided quotient rings are two-sided, Proc. Amer. Math. Soc. 15 (1963), 141–147.Google Scholar
14. Utumi, Y., On continuous rings and self infective rings, Trans. Amer. Math. Soc. 118 (1965), 158–173.Google Scholar
15. Utumi, Y., On the continuity and self-injectivity of a complete regular ring, Can. J. Math. 18 1966), 404–412.Google Scholar