Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T05:19:16.064Z Has data issue: false hasContentIssue false
  • English
  • Français

The Equivariant Grothendieck Groups of the Russell-Koras Threefolds

Published online by Cambridge University Press:  20 November 2018

J. P. Bell
J. P. Bell*
Affiliation:
Department of Mathematics, University of California, San Diego, 9500 Gilman Drive, Mailcode 0112, La Jolla, California 92093-0112, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Russell-Koras contractible threefolds are the smooth affine threefolds having a hyperbolic 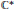${{\mathbb{C}}^{*}}$-action with quotient isomorphic to the corresponding quotient of the linear action on the tangent space at the unique fixed point. Koras and Russell gave a concrete description of all such threefolds and determined many interesting properties they possess. We use this description and these properties to compute the equivariant Grothendieck groups of these threefolds. In addition, we give certain equivariant invariants of these rings.

Keywords

14J3019L47
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 1 , 01 February 2001 , pp. 3 - 32
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Bass, H. and Haboush, W., Linearizing certain reductive group actions. Trans. Amer.Math. Soc. (2) 292(1985), 463–482.Google Scholar
[2] Bass, H. and Haboush, W., Some Equivariant K-theory of Affine Algebraic group actions. Comm. Algebra. (1–2) 15(1987), 181–217.Google Scholar
[3] Bourbaki, N., Commutative Algebra, Chapters 1–7. Springer-Verlag, New York, 1989.Google Scholar
[4] Eisenbud, D., Commutative Algebra with a view toward Algebraic Geometry. Springer-Verlag, New York, 1995.Google Scholar
[5] Kaliman, S. and Makar-Limanov, L., On the Russell-Koras contractible threefolds. J. AlgebraicGeom. 6(1997), 247–268.Google Scholar
[6] Knop, F., Nichtlinearisierbare Operationen halbeinfacher Gruppen auf affinen Räumen. Invent.Math. 105(1991), 217–220.Google Scholar
[7] Koras, M. and Russell, P., Contractible threefolds and C*-actions on C3. J. Algebraic Geom. (4) 6(1997), 671–695.Google Scholar
[8] Lam, T. Y., Serre's Conjecture. Lecture Notes in Mathematics 635. Springer-Verlag, Berlin-New York, 1978.Google Scholar
[9] Lang, S., Algebra 3rd ed. Addison-Wesley Pub. Co., Reading, Massachusetts, 1993.Google Scholar
[10] Masuda, M., Moser-Jauslin, L. and Petrie, T., The Equivariant Serre Problem for Abelian Groups. Topology (2) 35(1996), 329–334.Google Scholar
[11] Matsumura, H., Commutative Algebra, 2nd ed. Benjamin/Cummings Pub. Co., Reading, Massachusetts, 1980.Google Scholar
[12] Mohan Kumar, N. and Murthy, M. P., Algebraic cycles and vector bundles over affine three-folds. Ann. of Math. 116(1982), 579–591.Google Scholar
[13] Quillen, D., Higher algebraic K-theory: I. Algebraic K-theory. Battelle Conference, 1972, vol. I, Lecture Notes in Math. 341, Springer-Verlag, Berlin, 1973.Google Scholar
[14] Schwarz, Gerald W., Exotic Algebraic Group Actions. C. R. Acad. Sci. Paris Sér. I Math. (2) 309(1989), 89–94.Google Scholar