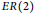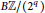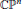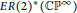Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kitchloo, Nitu
Lorman, Vitaly
and
Stephen Wilson, W.
2020.
The ER(2)-cohomology of ∏nCP∞ and BU(n).
Topology and its Applications,
Vol. 270,
Issue. ,
p.
106955.
Balderrama, William
2024.
The real-oriented cohomology of infinite stunted projective spaces.
Algebraic & Geometric Topology,
Vol. 24,
Issue. 7,
p.
4061.