Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-11T03:26:17.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact Values for Degree Sums Over Strips of Young Diagrams

Published online by Cambridge University Press:  20 November 2018

I. P. Goulden
I. P. Goulden*
Affiliation:
Department of Combinatorics & Optimization, University of Waterloo, Waterloo, Ontario, N2L 3G1
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If λ = (λ1,…, λm) where λ1,…,λm are nonnegative integers with λ1 ≥…≥ λm, then λ is a partition of |λ| = λ1 + …+λm, and we write λ⊢ |λ|. The non-zero λi's are the parts of λ, so λ1 is the largest part, and ℓ(λ) is the number of parts of λ. Two partitions with the same parts, so they differ only in number of zeros, are the same. The set of all partitions, including the partition of 0 (with 0 parts) is denoted by 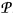The conjugate of λ, denoted by 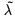, is the partition (μ1,…, μk), in which μi is the number of λ's that are ≥i , for i = 1,…, k, where k=λ1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 5 , 01 October 1990 , pp. 763 - 775
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Bender, E. A. and Knuth, D. E., Enumeration of plane partitions, J. Combin. Theory Ser. A13 (1972), 40–54.Google Scholar
2. Frame, J. S., Robinson, G. de B. and Thrall, R. M., The hook graphs of Sn , Canad. J. Math. 6 (1954), 316-324.Google Scholar
3. Gessel, I. M., Symmetric functions and p-recursiveness, J. Combin. Theory Ser. A (to appear).Google Scholar
4. Gordon, B., Notes on plane partitions V, J. Combin. Theory 11 (1971), 157–168.Google Scholar
5. Gordon, B. and Houten, L., Notes on plane partitions II, J. Combin. Theory 4 (1968), 81–99.Google Scholar
6. Gouyou-Beauchamps, D., Standard Young tableaux of height 4 and 5, European J. Comb, (to appear).Google Scholar
7. Knuth, D. E., The art of computer programming, 3 Addison-Wesley, Reading, Mass., 1968.Google Scholar
8. Latyshev, V. H., On the theorem of Regev about identities in the tensor product of P. I. algebras, Uspekhi Mat. Nauk. (1972), 213–214.Google Scholar
9. Macdonald, I. G., Symmetric functions and Hall polynomials, Clarendon Press, Oxford, 1979.Google Scholar
10. Procesi, C., The invariant theory of n x n matrices, Adv. in Math. 19 (1976), 306–381.Google Scholar
11. Procesi, C. Trace identities and standard diagrams, Ring Theory, Proc. of the 1978 Antwerp Conference (Van Oystaeyan F., Ed.).Google Scholar
12. Razmyslov, Ju. P., Trace identities of full matrix algebras over a field of characteristic zero, Izv. Akad. Nauk. SSSR No. 4, 1974.Google Scholar
13. Regev, A., Asymptotic values for degrees associated with strips of Young diagrams, Adv. in Math. 41, (1981), 115–136.Google Scholar
14. Schensted, C., Longest increasing and decreasing subsequences, Canad. J. Math. 13, (1961), 179–191.Google Scholar
15. Schur, I., Über eine klasse von matrizen, die sich einer gegebenen matrix zuordnen lassen, Dissertation, Berlin, 1901, (Reprinted in Gesammelte Abhandlungen, Springer-Verlag, 1973.)Google Scholar
16. Stanley, R. P., Theory and applications of plane partitions I, II, Studies Applied Math. 50, (1971), 167-188, 259–279.Google Scholar
17. Stanley, R. P. Dijferentiably finite power series, Europ. J. Combin. 1 (1980), 175–188.Google Scholar