No CrossRef data available.
Article contents
The Extensions of an Invariant Mean and the Set LIM ∽ TLIM
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 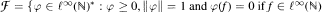 with
with 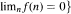 . If G is a nondiscrete locally compact group which is amenable as a discrete group and m ∈ LIM(CB(G)), then we can embed
. If G is a nondiscrete locally compact group which is amenable as a discrete group and m ∈ LIM(CB(G)), then we can embed 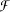 into the set of all extensions of m to left invariant means on L∞(G) which are mutually singular to every element of TLIM(L∞(G)), where LIM(S) and TLIM(S) are the sets of left invariant means and topologically left invariant means on S with S = CB(G) or L∞(G). It follows that the cardinalities of LIM(L∞(G)) ̴ TLIM(L∞(G)) and LIM(L∞(G)) are equal. Note that
into the set of all extensions of m to left invariant means on L∞(G) which are mutually singular to every element of TLIM(L∞(G)), where LIM(S) and TLIM(S) are the sets of left invariant means and topologically left invariant means on S with S = CB(G) or L∞(G). It follows that the cardinalities of LIM(L∞(G)) ̴ TLIM(L∞(G)) and LIM(L∞(G)) are equal. Note that 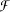 which contains
which contains 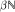 is a very big set. We also embed
is a very big set. We also embed 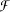 into the set of all left invariant means on CB(G) which are mutually singular to every element of TLIM(CB(G)) for G = G1 ⨯ G2, where G1 is nondiscrete, non–compact, σ–compact and amenable as a discrete group and G2 is any amenable locally compact group. The extension of any left invariant mean on UCB(G) to CB(G) is discussed. We also provide an answer to a problem raised by Rosenblatt.
into the set of all left invariant means on CB(G) which are mutually singular to every element of TLIM(CB(G)) for G = G1 ⨯ G2, where G1 is nondiscrete, non–compact, σ–compact and amenable as a discrete group and G2 is any amenable locally compact group. The extension of any left invariant mean on UCB(G) to CB(G) is discussed. We also provide an answer to a problem raised by Rosenblatt.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1994


