Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-27T11:14:19.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Point and Edge Sets in n-Graphs

Published online by Cambridge University Press:  20 November 2018

N. Sauer
N. Sauer*
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A set of points (edges) of a graph is independent if no two distinct members of the set are adjacent. Gallai (1) observed that, if A0 (B0) is the minimum number of points (edges) of a finite graph covering all the edges (points) and A1 (B1) is the maximum number of independent points (edges), then:

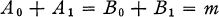
holds, where m is the number of points of the graph.

The concepts of independence and covering are generalized in various ways for n-graphs. In this paper we establish certain connections between the corresponding extreme numbers analogous to the above result of Gallai.

Ray-Chaudhuri considered (2) independence and covering problems in n-graphs and determined algorithms for finding the minimal cover and some associated numbers.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1069 - 1075
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Gallai, T., Über extreme Punkt- und Kantenmengen, Ann. Univ. Sci. Budapest Eôtvôs Sect. Math. 2 (1959), 133–138.Google Scholar
2. Ray-Chaudhuri, D. K., An algorithm for a minimum cover of an abstract complex, Can. J. Math. 15 (1963), 11–24.Google Scholar