Article contents
Extremal Problems for Functions Starlike in the Exterior of the Unit Circle
Published online by Cambridge University Press: 20 November 2018
Extract
Let Σ represent the class of analytic functions
(1)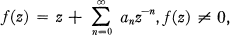
which are regular, except for a simple pole at infinity, and univalent in |z| > 1 and map |z| > 1 onto a domain whose complement is starlike with respect to the origin. Further let Σ- 1 be the class of inverse functions of Σ which at w = ∞ have the expansion
(2)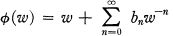 .
.
In this paper we develop variational formulas for functions of the classes Σ and Σ- 1 and obtain certain properties of functions that extremalize some rather general functionals pertaining to these classes. In particular, we obtain precise upper bounds for |b2| and |b3|. Precise upper bounds for |b1|, |b2 | and |b3| are given by Springer (8) for the general univalent case, provided b0 =0.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1962
References
- 5
- Cited by

