Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T14:14:32.635Z Has data issue: false hasContentIssue false
  • English
  • Français

Extremal Problems for the Classes SR-p and TR-p

Published online by Cambridge University Press:  20 November 2018

Walter Hengartner  and
Wojciech Szapiel
Walter Hengartner
Affiliation:
Département de Mathématiques, Université Laval, Québecy P.Q., Canada
Wojciech Szapiel
Affiliation:
Institute of Mathematics, M. Curie - Sklodowska University, Lublin, Poland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let H(D) be the linear space of analytic functions on a domain D of ℂ endowed with the topology of locally uniform convergence and let H‘(D) be the topological dual space of H(D). For domains D which are symmetric with respect to the real axis we use the notation 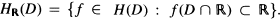Furthermore, denote by S the set of all univalent mappings f defined on the unit disk Δ which are normalized by f (0) = 0 and f‘(0) =1.

Keywords

30C45
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 4 , 01 August 1990 , pp. 619 - 645
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Brickman, L., Extreme points of the set of univalent functions, Bull. Amer. Soc. 76 (1970), 372–374.Google Scholar
2. Brickman, L., MacGregor, T.H., Wilken, D., Convex hulls of some classical families of univalentfunctions, Trans. Amer. Math. Soc. 156 (1971), 91–107.Google Scholar
3. Duren, P.L., Univalent functions, Springer- Verlag Berlin, 1983.Google Scholar
4. Duren, P.L., Schober, G., Nonvanishing univalent Junctions, Math. Z. 170 (1980), 195–216.Google Scholar
5. Goluzin, M.G., Geometric theory of functions of a complex variable, Translations of Math. Monographs, 26, Amer. Math. Soc. Providence, Rhode Island, 1969.Google Scholar
6. Koepf, W., On nonvanishing univalent functions with real coefficients, Math. Z. 192 (1986), 575–579.Google Scholar
7. Schober, G., Univalent functions - selected topics. Lecture Notes 478, Springer-Verlag Berlin, 1975.Google Scholar
8. Szapiel, W., Points extrémaux dans les ensembles convexes 1. Théorie générale, Bull. Acad. Polon. Sci., Math. 23 (1975), 939–945.Google Scholar
9. Szapiel, W., Extreme points of convex sets 2. Influence of normalisation on integral representations,, Bull. Acad. Polon. Sci., Math 29 (1981), 535–544.Google Scholar
10. Szapiel, W., Extreme points of convex sets 3. Montel's normalisation, Bull. Acad. Polon. Sci., Math. 30 (1982), 41–47.Google Scholar
11. Szapiel, M., Szapiel, W., Extreme points of convex sets 4. Bounded typically real functions, Bull. Acad. Polon. Sci., Math 30 (1982), 49–57.Google Scholar
12. Tammi, O., Extremum problems for bounded univalent functions, Lecture Notes 646, Springer- Veriag Berlin, 1978.Google Scholar