Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T07:41:41.631Z Has data issue: false hasContentIssue false
  • English
  • Français

A Family of Real Pn-Tic Fields

Published online by Cambridge University Press:  20 November 2018

Yuan-Yuan Shen  and
Lawrence C. Washington
Yuan-Yuan Shen
Affiliation:
Department of Mathematics, Tunghai University Taichung, Taiwan 40704, R.O.C.
Lawrence C. Washington
Affiliation:
Department of Mathematics, University of Maryland, College Park, Maryland 20742, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let q = p if p is an odd prime, q = 4 if p = 2. Let ζq be any primitive q-th root of unity, and let 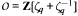. We study the family of polynomials 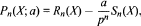where Rn(X) and Sn(X) are the polynomials in the expansion 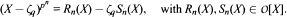We show that for fixed n, Pn(X; a) is irreducible for all but finitely many a ∈ O, and for p = 3, we show that it is irreducible for all a ∈ O. The roots are all real and are permuted cyclically by a linear fractional transformation defined over the real pn-th cyclotomic field. From the roots we obtain a non-maximal set of independent units for the splitting field. In the last section we briefly treat extensions of our methods to composite p.

Keywords

11R2111R0911R1611R1811R27pn-tic fieldsunits
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 3 , 01 June 1995 , pp. 655 - 672
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Cremona, J.E., Algorithms for Modular Elliptic Curves, Cambridge University Press, New York, 1992.Google Scholar
2. Gras, Marie-Nicole, Special units in real cyclic sextic fields, Math. Comp. 48(1987), 179–182.Google Scholar
3. Gras, Marie-Nicole, Familles d'unités dans les extensions cycliques réelles de degré 6 de Q, Publ. Math. Besançon, 1984.1985-1985/86.Google Scholar
4. Hemer, O., Notes on the Diophantine equation y2 — k =, x3, Ark. Mat. 3(1954), 67–77.Google Scholar
5. Lang, Serge, Algebra, Addison-Wesley, Reading, Massachusetts, 1965.Google Scholar
6. Shanks, D., The simplest cubic fields, Math. Comp. 28(1974), 1137–1152.Google Scholar
7. Shen, Y.-Y. and Washington, L.C., A family of real 2n-tic fields, to appear.Google Scholar