Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-13T05:51:57.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Federer-Čech Couples

Published online by Cambridge University Press:  20 November 2018

Micheal Dyer
Micheal Dyer*
Affiliation:
University of Oregon, Eugene, Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (5),I considered two-term conditions in π-exact couples, of which the exact couple 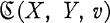of Federer (7) is an example. Let M(X, Y)be the space of all maps from X to Y with the compact-open topology. Our aim in this paper is to construct a π-exact couple 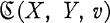, where Xis a finite-dimensional (in the sense of Lebesgue) metric space and 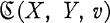, a certain (rather large) class of spaces. Specifically, 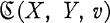is the class of all topological spaces Xwhich possess the following property (P).

(P) Let Y be a (possibly infinite) simplicial complex. There exists x0 ∈ X and y0 ∊ Y such that [X, x0]≃ [Y, y0].

In § 5 it will be seen that 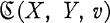contains all CW complexes and all metric absolute neighbourhood retracts (ANR)s.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 842 - 864
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Barratt, M., Track groups. II, Proc. London Math. Soc. 5 (1955), 285–329 Google Scholar
2. Dowker, C. H., Mapping theorems for non-compact spaces, Amer. J. Math. 69 (1947), 200–242.Google Scholar
3. Dowker, C. H., On countably paracompact spaces, Can. J. Math. 3 (1951), 219–224.Google Scholar
4. Dowker, C. H., Homotopy extension theorems, Proc. London Math. Soc. (3) 6 (1956), 100–116.Google Scholar
5. Dyer, M., Two term conditions in T exact couples, Can. J. Math. 19 (1967), 1263–1288.Google Scholar
6. Eilenberg, S. and Steenrod, N., Foundation of algebraic topology (Princeton Univ. Press, Princeton, N.J., 1952).Google Scholar
7. Fédérer, H., A study of function spaces by spectral sequences, Trans. Amer. Math. Soc. 82 (1956), 340–361.Google Scholar
8. Hu, S.-T., Homotopy theory (Academic Press, New York, 1959).Google Scholar
9. Hu, S.-T., Homology theory (Holden Day, San Francisco, 1966).Google Scholar
10. Hu, S.-T., Theory of retracts (Wayne State Univ. Press, Detroit, Michigan, 1965).Google Scholar
11. Lee, C. N. and Raymond, F., Cech Extensions of contravariant functors (to appear).Google Scholar
12. Milnor, J., On spaces having the homotopy type of a CW complex, Trans. Amer. Math. Soc. 90 (1959), 272–290.Google Scholar
13. Mimura, M., The homotopy groups of lie groups of low rank, J. Math. Kyoto Univ. 6 (1967), 131–176.Google Scholar
14. Spanier, E., Borsuk's cohomotopy groups, Ann. of Math. 50 (1949), 203–245.Google Scholar
15. Steenrod, N., Cohomology operations, lectures by Steenrod, N., written and revised by Epstein, D. B. A., Annals of Math. Studies, No. 50 (Princeton Univ. Press, Princeton, N.J., 1962).Google Scholar
16. Toda, H., Composition methods in homotopy groups of spheres, Annals of Math. Studies, No. 49 (Princeton Univ. Press, Princeton, N.J., 1962).Google Scholar
17. Whitehead, G. W., Homotopy groups of joins and unions, Trans. Amer. Math. Soc. 83 (1956), 55–69.Google Scholar
18. Whitehead, J. H. C., A note on a theorem due to Boursuk, Bull. Amer. Math. Soc. 54 (1948), 1125–1132.Google Scholar
19. Whitehead, J. H. C., Combinatorial homotopy. I, Bull. Amer. Math. Soc. 55 (1949), 213–235 Google Scholar