Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maranda, J.-M.
1968.
Études sur les Groupes abéliens / Studies on Abelian Groups.
p.
267.
Tsalenko, M. S.
and
Shul’geifer, E. G.
1971.
Progress in Mathematics.
p.
3.
Palmquist, Paul H.
1971.
Reports of the Midwest Category Seminar V.
Vol. 195,
Issue. ,
p.
123.
Fisher-Palmquist, Janet
and
Newell, David C
1973.
Triples on functor categories.
Journal of Algebra,
Vol. 25,
Issue. 2,
p.
226.
Marquis, Jean-Pierre
and
Reyes, Gonzalo E.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
689.
Arkor, Nathanael
and
McDermott, Dylan
2024.
The formal theory of relative monads.
Journal of Pure and Applied Algebra,
Vol. 228,
Issue. 9,
p.
107676.


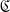 is made up of its class of objects
is made up of its class of objects 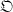 , of a function
, of a function 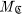 ) which assigns to each (
) which assigns to each (