Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-11T08:56:01.251Z Has data issue: false hasContentIssue false
  • English
  • Français

Formal Fibers of Unique Factorization Domains

Published online by Cambridge University Press:  20 November 2018

Adam Boocher ,
Michael Daub ,
Ryan K. Johnson ,
H. Lindo ,
S. Loepp  and
Paul A. Woodard
Adam Boocher
Affiliation:
University of California, Berkeley, CA 94709, USA, e-mail: aboocher@math.berkeley.edu, mwdaub@math.berkeley.edu
Michael Daub
Affiliation:
University of California, Berkeley, CA 94709, USA, e-mail: aboocher@math.berkeley.edu, mwdaub@math.berkeley.edu
Ryan K. Johnson
Affiliation:
Williams College, Williamstown, Massachusetts 01267, USA, e-mail: 08hml@williams.edu, sloepp@williams.edu, 08paw@williams.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 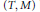$\left( T,\,M \right)$ be a complete local (Noetherian) ring such that 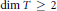$\dim\,T\,\ge \,2$ and 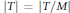$\left| T \right|\,=\,\left| T/M \right|$ and let 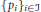${{\left\{ {{p}_{i}} \right\}}_{i\in \Im }}$ be a collection of elements of 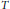$T$ indexed by a set 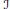$\mathcal{J}$ so that 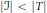$\left| \mathcal{J} \right|\,<\,\left| T \right|$. 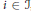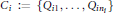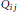For each $i\,\in \,\mathcal{J}$, let ${{C}_{i}}:=\left\{ {{Q}_{i1}},...,{{Q}_{i{{n}_{i}}}} \right\}$ be a set of nonmaximal prime ideals containing ${{p}_{i}}$ such that the ${{Q}_{ij}}$ are incomparable and 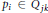${{p}_{i}}\in {{Q}_{jk}}$ if and only if 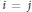$i\,=\,j$. We provide necessary and sufficient conditions so that 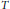$T$ is the 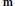$\mathbf{m}$-adic completion of a local unique factorization domain 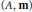$\left( A,\,\mathbf{m} \right)$, and for each 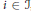$i\,\in \,\mathcal{J}$, there exists a unit ${{t}_{i}}$ of 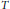$T$ so that 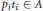${{p}_{i}}{{t}_{i}}\in A$ and 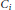${{C}_{i}}$ is the set of prime ideals 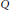$Q$ of 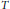$T$ that are maximal with respect to the condition that 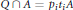$Q\cap A={{p}_{i}}{{t}_{i}}A$.

We then use this result to construct a (nonexcellent) unique factorization domain containing many ideals for which tight closure and completion do not commute. As another application, we construct a unique factorization domain 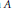$A$ most of whose formal fibers are geometrically regular.

Keywords

13J1013J05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 4 , 01 August 2010 , pp. 721 - 736
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Bryk, J., Mapes, S., Samuels, C., and G.Wang, Constructing almost excellent unique factorization domains. Comm. Algebra 33(2005), no. 5, 1321–1336. doi:10.1081/AGB-200058363Google Scholar
[2] Charters, P. and Loepp, S., Semilocal generic formal fibers. J. Algebra 278(2004), no. 1, 370–382. doi:10.1016/j.jalgebra.2004.01.011Google Scholar
[3] Chatlos, J., Simanek, B., Watson, N. G., and S. X., Wu. Semilocal formal fibers of principal prime ideals. http//front.math.ucdavis.edu/0911.4196.Google Scholar
[4] Heitmann, R. C., Characterization of completions of unique factorization domains. Trans. Amer. Math. Soc. 337(1993), no. 1, 379–387. doi:10.2307/2154327Google Scholar
[5] Heitmann, R. C., Completions of local rings with an isolated singularity. J. Algebra 163(1994), no. 2, 538–567. doi:10.1006/jabr.1994.1031Google Scholar
[6] Huneke, C., Tight Closure and Its Applications. With an appendix by Melvin Hochster. CB MS Regional Conference Series in Mathematics 88. American Mathematical Society, Providence, RI, 1996.Google Scholar
[7] Lipman, J., Rational singularities, with applications to algebraic surfaces and unique factorization. Inst. Hautes Études Sci. Publ. Math. (1969), No. 36, 195–279.Google Scholar
[8] Loepp, S., Constructing local generic formal fibers. J. Algebra 187(1997), no. 1, 16–38. doi:10.1006/jabr.1997.6768Google Scholar
[9] Loepp, S., Characterization of completions of excellent domains of characteristic zero. J. Algebra 265(2003), no. 1, 221–228. doi:10.1016/S0021-8693(03)00239-4Google Scholar
[10] Loepp, S. and Rotthaus, C., Some results on tight closure and completion. J. Algebra 246(2001), no. 2, 859–880. doi:10.1006/jabr.2001.9006Google Scholar
[11] Matsumura, H., Commutative Ring Theory. Second edition. Cambridge Studies in Advanced Mathematics 8. Cambridge University Press, Cambridge, 1989.Google Scholar
[12] Sharp, R. Y., Steps in Commutative Algebra. Second edition. London Mathematical Society Student Texts 51. Cambridge University Press, Cambridge, 2000.Google Scholar