Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T15:17:08.420Z Has data issue: false hasContentIssue false
  • English
  • Français

Fully Nonlinear Elliptic Equations on General Domains

Published online by Cambridge University Press:  20 November 2018

Jiguang Bao
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By means of the Pucci operator, we construct a function 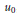${{u}_{0}}$, which plays an essential role in our considerations, and give the existence and regularity theorems for the bounded viscosity solutions of the generalized Dirichlet problems of second order fully nonlinear elliptic equations on the general bounded domains, which may be irregular. The approximation method, the accretive operator technique and the Caffarelli's perturbation theory are used.

Keywords

35D0535D1035J6035J67Pucci operatorviscosity solutionexistenceC2,ψ regularityDini conditionfully nonlinear equationgeneral domainaccretive operatorapproximation lemma
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 6 , 01 December 2002 , pp. 1121 - 1141
Copyright
Copyright © Canadian Mathematical Society 2002

Footnotes

*

Permanent address: Department of Mathematics, Beijing Normal University, Beijing, 100875, People's Republic of China e-mail: jgbao@bnu.edu.cn

References

[B1] Bao, J., viscosity solutions of Neumann problems for fully nonlinear elliptic equations. J. Partial Differential Equations 8 (1995), 219–232.Google Scholar
[B2] Bao, J., Solvability of Semilinear Elliptic Equations on General Domains. Nonlinear Anal., to appear.Google Scholar
[Ba] Barbu, V., Nonlinear Semigroups and Differential Equations in Banach Spaces. Noordhooff International Publishing, Leyden, 1976.Google Scholar
[Bi] Bian, B. J., Existence of viscosity solutions of second order fully nonlinear elliptic equations. J. Partial Differential Equations 4 (1991), 21–32.Google Scholar
[Bu] Burch, C., The Dini condition and regularity of weak solutions of elliptic equations. J. Differential Equations 30 (1978), 308–323.Google Scholar
[BNV] Berestycki, H., Nirenberg, L. and Varadhan, S. R. S., The principal eigenvalue and maximum principle for second order elliptic operators in general domains. Comm. Pure Appl. Math. 47 (1994), 47–92.Google Scholar
[C] Caffarelli, L. A., Interior a priori estimates for solutions of fully nonlinear equations. Ann. of Math. 130 (1989), 189–213.Google Scholar
[CC] Caffarelli, L. A. and Cabre, X., Fully nonlinear elliptic equations. Colloquium publications 43, Amer. Math. Soc., Providence, Rhode Island, 1995.Google Scholar
[CIL] Crandall, M. G., Ishii, H. and Lions, P. L., User's guide to viscosity solutions of second order partial differential equations. Bull. Amer.Math. Soc. 27 (1992), 1–67.Google Scholar
[CJ] Chang, K. C. and Jiang, M. Y., Parabolic equations and the Feynman-Kac formula on general bounded domains. Research report 27, Institute of Mathematics, Peking University, 1999.Google Scholar
[CZ] Chen, Y. Z. and Zou, X., Fully nonlinear parabolic equations and Dini condition. preprint.Google Scholar
[E1] Evans, L. C., A convergence theorem for solutions of nonlinear second order elliptic equations. Indiana Univ.Math. J. 27 (1978), 875–887.Google Scholar
[E2] Evans, L. C., On solving certain nonlinear partial differential equations by accretive operator methods. Israel J. Math. 36 (1980), 225–247.Google Scholar
[GT] Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order. Second ed., Springer-Verlag, Berlin, 1983.Google Scholar
[I] Ishii, H., On the uniqueness and existence of viscosity solutions of fully nonlinear second order elliptic PDE's. Comm. Pure Appl. Math. 42 (1989), 14–45.Google Scholar
[K1] Kovats, J., Fully nonlinear elliptic equations and the Dini condition. Comm. Partial Differential Equations 22 (1997), 1911–1927.Google Scholar
[K2] Kovats, J., Dini-Campanato spaces and applications to nonlinear elliptic equations. Electron. J. Differential Equations 37(1999), 20pp.Google Scholar
[M] Michael, J. H., Barriers for uniformly elliptic equations and the exterior cone condition. J. Math. Anal. Appl. 79 (1981), 203–217.Google Scholar
[P] Padilla, P., The principal eigenvalue and maximum principle for second order elliptic operators on Riemann manifolds. J Math. Anal. Appl. 205 (1997), 285–312.Google Scholar
[SV] Stroock, D. and Varadhan, S. R. S., On degenerate elliptic-parabolic operator of second order and their associated diffusions. Comm. Pure Appl. Math. 25 (1972), 651–713.Google Scholar
[T] Trudinger, N. S., Fully nonlinear, uniformly elliptic equations under natural structure conditions. Trans. Amer.Math. Soc. 278 (1983), 751–769.Google Scholar